求逆序对数量与归并排序

发表于

逆序对统计

最近写算法题的时候又遇到了这类问题:
在数组中的两个数字，如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数P。
输入：1,2,3,4,5,6,7,0
输出： 7
可以从上面得知，逆序对分别为：<1,0> <2,0> <3,0> <4,0> <5,0> <6,0> <7,0>
这里问题，一个所有人都能想到的求解方法就是暴力搜索：用两层for循环将数组中的元素全部两两比较一遍，就能得到所有的逆序对数。
当然这样的做法也不是不行，但是效果是时间效率非常的低下，时间复杂度是O(n^2);在数据量很大的时候，响应时间会非常的久，这在算法上是不能接受的。
今天我们学习另一种思想：Divide And Conquer(分而治之—分治思想)，它的核心思想就是：大事化小，通过解决多个子问题来解决大问题。
这个问题的解决思路是和归并排序的思想类似的。
话不多说先看代码： （可以用归并排序来作为带入）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
public class 数组逆向序对 {
    public static void main(String[] args) {
        数组逆向序对 nx = new 数组逆向序对();
        int[] a = {1, 2, 3, 4, 5, 6, 7, 0};
        System.out.println(nx.InversePairs(a));
    }

    public int InversePairs(int[] array) {
        int n = array.length;
        int[] temp = new int[n];
        long ans = MergeSortAndCount(array, 0, n - 1, temp);
        return (int) ans;
    }

    public long MergeSortAndCount(int[] array, int left, int right, int[] temp) {
        if (left >= right) return 0;
        int mid = (left + right) / 2;
        long count1 = MergeSortAndCount(array, left, mid, temp);
        long count2 = MergeSortAndCount(array, mid + 1, right, temp);
        long count3 = MergeAndCount(array, left, mid, right, temp);
        return (count1 + count2 + count3) % 1000000007;
    }

    public long MergeAndCount(int[] array, int left, int mid, int right, int[] temp) {
        int i = left;
        int j = mid + 1;
        int k = left;
        long cnt = 0;

        while (i <= mid && j <= right) {
            if (array[i] <= array[j]) {
                temp[k++] = array[i++];
            } else {
                temp[k++] = array[j++];
                cnt += mid - i + 1;    // 关键步骤，进行计数
            }
        }

        while (i <= mid) temp[k++] = array[i++];
        while (j <= right) temp[k++] = array[j++];

        for (i = left; i <= right; ++i) {
            array[i] = temp[i];
        }
        return cnt;
    }

}

直接去读这段代码还是有些吃力的，主要有递归程序在，容易把我们绕晕，所以我们以归并排序作为基本思想，来慢慢解决这个问题：

归并排序

归并排序，中国人翻译算法的名字的时候通常使用它们的具体含义来命名，这里归并排序也不理外，很容易理解的是，这个排序算法找中肯定包含着：归类与合并，这两个步骤。
归类处理，然后合并，这种思想就是分治——分而治之也就是Divide and conquer。

归并排序的主要思想

我们上面的找逆序对的问题，其实就是一个简单的归并排序问题，如果你能够充分的理解归并排序，那么上面的找逆序对的问题就不是什么难题。
对于排序，我们知道，它最终的目的是将数据进行有序化，是会对数据进行位置交换的算法。（归并排序是一种稳定的排序算法）。它是通过将一个长度为n的数组分成左右两个部分，通常以n/2作为
下面我们通过简单的例子来进行讲解，会做到详尽周到，希望能对自己和他人的理解有所帮助。

实例

比如我们有一个数组包含4个元素[4,1,2,3]，我们希望通过归并排序，将这个数组进行排序。
我们可以通过下面的代码进行实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
public class 数组逆向序对 {
    public static void main(String[] args) {
        数组逆向序对 nx = new 数组逆向序对();
        int[] a = [4,1,2,3};
        System.out.println(nx.InversePairs(a));
    }

    public int InversePairs(int[] array) {
        int n = array.length;
        int[] temp = new int[n];
        long ans = MergeSortAndCount(array, 0, n - 1, temp);
        return (int) ans;
    }

    public long MergeSortAndCount(int[] array, int left, int right, int[] temp) {
        if (left >= right) return 0;
        int mid = (left + right) / 2;
        long count1 = MergeSortAndCount(array, left, mid, temp);
        long count2 = MergeSortAndCount(array, mid + 1, right, temp);
        long count3 = MergeAndCount(array, left, mid, right, temp);
        return (count1 + count2 + count3) % 1000000007;
    }

    public long MergeAndCount(int[] array, int left, int mid, int right, int[] temp) {
        int i = left;
        int j = mid + 1;
        int k = left;
        long cnt = 0;

        while (i <= mid && j <= right) {
            if (array[i] <= array[j]) {
                temp[k++] = array[i++];
            } else {
                temp[k++] = array[j++];
            }
        }

        while (i <= mid) temp[k++] = array[i++];
        while (j <= right) temp[k++] = array[j++];

        for (i = left; i <= right; ++i) {
            array[i] = temp[i];
        }
        return cnt;
    }

}

这个代码与我们上面缩写的代码仅仅少一行 cnt += mid - i + 1;。而他们的实现过程是一模一样的，我们一点点对代码进行分析。
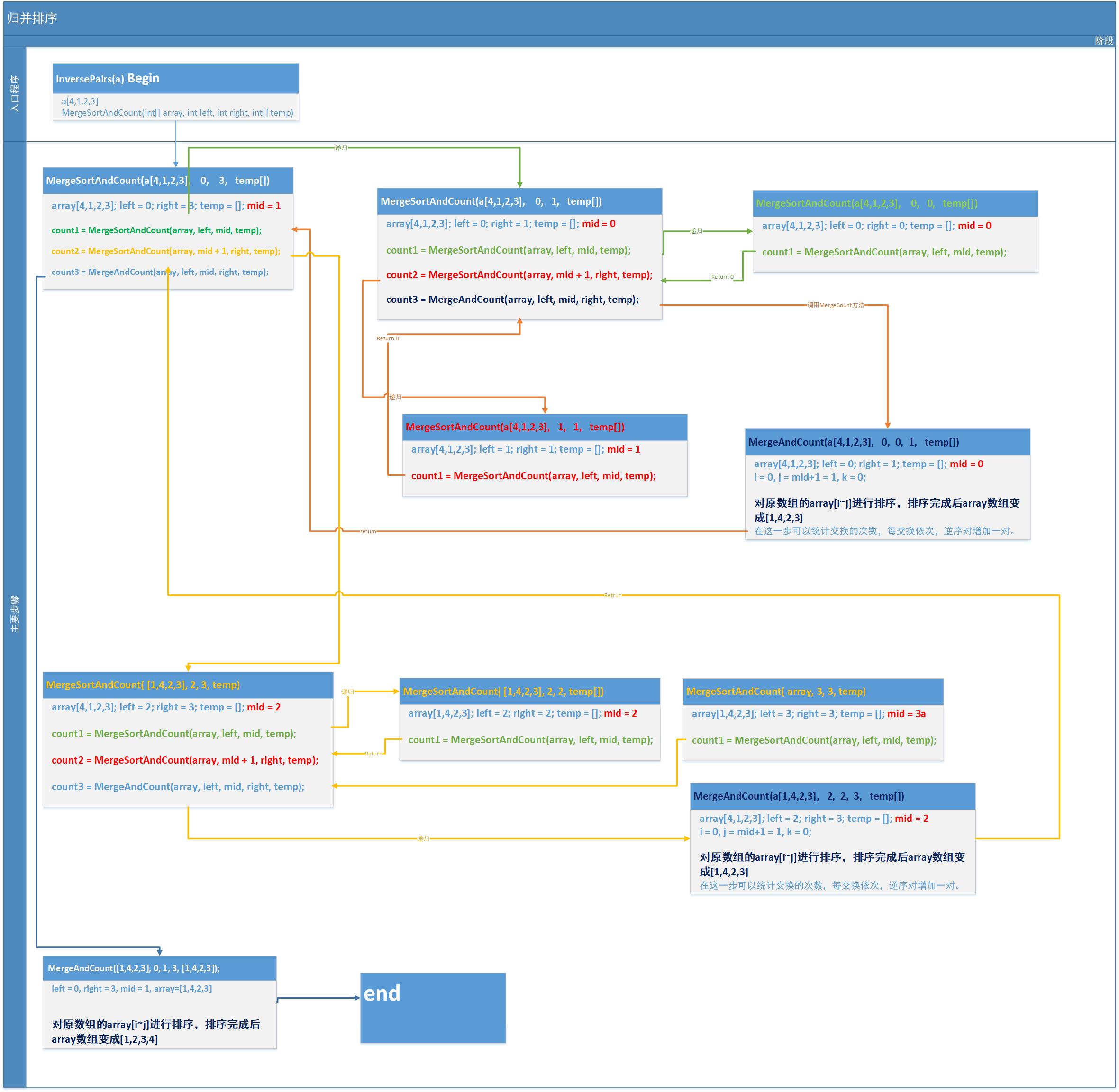
我们从InversePairs开始：它调用了MergeSortAndCount方法，而MergeSortAndCount方法又调用了MergeAndCount方法。这中间涉及到递归调用，用脑子想的办法去理解可能会有些复杂，我花了一个逻辑调用图，来帮助我们理解归并排序。 归并排序的要点在于，一个是递归，一个是将左右两个部分进行对比排序，如果没有这个递归操作，那么仅仅能保证整个数组以mid为中心，右边比左边大，但是不能保证左右两侧都是有序的，带上递归后，左右两侧分别一直进行递归比较操作，知道这个小的比较区域只剩两个元素，也就完成了子区间的比较。
MergeSort

Donate comment here