WebGL

发表于 | 分类于

WebGL基础与应用

新的技术啊，没人引导，自己啃的话，一开始的时候真的会觉得无从下手，尤其新的领域的内容，有时会感觉力不从 心，但是相信功夫不负有心人，只有肯努力，一定能在这个领域有所建树的，加油！

对于webGL，它实际上是OpenGL的web实现，是HTML5标准之下，新出的一套web呈现技术，能够在浏览器端实现以前只有在桌面上才能实现的复杂图形图像。

通过这篇文章，来介绍学习过程，解决实际问题。
这次的问题是：如果将三维模型标准化，归一化，正常的显示在显示器上

模型矩阵，视图矩阵和投影矩阵

PS:这部分内容来源于model_view_projection
通常用于表示3D模型对象的三个核心矩阵就是：模型矩阵，视图矩阵，以及投影矩阵。下面我们详细介绍每个矩阵的用途，以及三者的联系。

空间中点和多边形的基本变换（如平移，缩放和旋转）由各种变换矩阵来处理。这些矩阵可以组合在一起，使它们可用于渲染复杂的3D场景。这些组合矩阵最终将原始模型数据移动到称为 剪辑空间(Clipspace) 的特殊坐标空间中。这是一个2单位宽的立方体。中心坐标为（0,0,0），而角点范围为（-1，-1，-1）至（1,1,1）。此剪辑空间被压缩到2d空间并光栅化为图像。

  1. 模型矩阵
    模型矩阵定义了如何获取原始模型数据，以及如何在三维世界坐标系中移动模型（ which defines how you take your original model data and move it around in 3d world space.）下一步，为了获取世界坐标系中的坐标，以及将模型移动到剪辑空间中（剪辑空间其实就是我们的可视区域），我们需要投影矩阵，而常用于投影的矩阵是透视矩阵（perspective matrix）它模仿的就是照相机的原理。最后如果需要移动相机，就又需要一个视图矩阵，用来移动相机。
  2. 剪辑空间（裁剪空间 Clipspace）
    剪辑空间也就是我们的可视区域，任何数据位于剪辑空间外的话，则会被剪掉，并且不会渲染。在一个WebGL程序中，模型数据通常会以它自己的坐标系上传到GPU，然后顶点着色器会将这些点转换到不同的坐标系系统下进行渲染。
    clipspace
    上图是所有点必须适合的剪辑空间的可视化。它是2个单位宽，由角（-1，-1，-1）到角（1,1,1）的立方体组成。立方体的中间是点（0,0,0）。
    这个空间就是剪辑空间或者叫裁剪空间。裁剪空间的目标是能够方便地对渲染图元进行裁剪：完全位于这块空间内部的图元将会被保留，完全位于这块空间外部的图元将会被剔除，而与这块空间边界相交的图元就会被裁剪。。那么，这块空间是如何决定的呢？答案是由视锥体(view frustum)来决定。

  3. 两种投影模式
    视锥体指的是空间中的一块区域，这块区域决定了摄像机可以看到的空间。视锥体由六个平面包围而成，这些平面也被称为 裁剪平面(clip planes)。视锥体有两种类型，这涉及两种投影类型：一种是 正交投影(orthographic projection)，一种是 透视投影(perspective projection)。
    透视投影:
    透视投影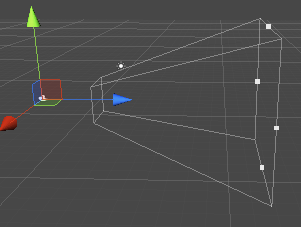

    正交投影:
    正交投影

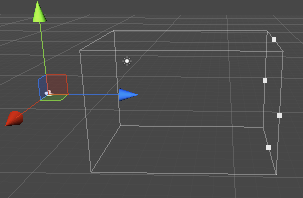
世界坐标系（World Coordinate System）

世界坐标系，我们可以看做是一个永恒不变的参考系，所以的其他模型，和各种坐标系都以这个坐标系作为基准。世界坐标系的位置不随模型的变化而改变。

模型坐标系 (Model Coordinate System)

模型坐标系是建模时所用到的坐标系，模型的原点为(0,0,0),但是它可以是世界坐标系中的任意一点。
通常在Three.js中，我们设置Object.position.set(0,0,0)就是将模型的原点设置为世界坐标系的原点。

  • 模型中心设置
    object.children[i].geometry.center(); //将网格模型的中心移动到世界坐标系的中心 这样做，对于单一Mesh构成的三维模型能够轻松将模型移动到世界坐标系中央，但是对于多Mesh构成的模型来讲，每个children的Mesh都会被移动到World坐标系原点。

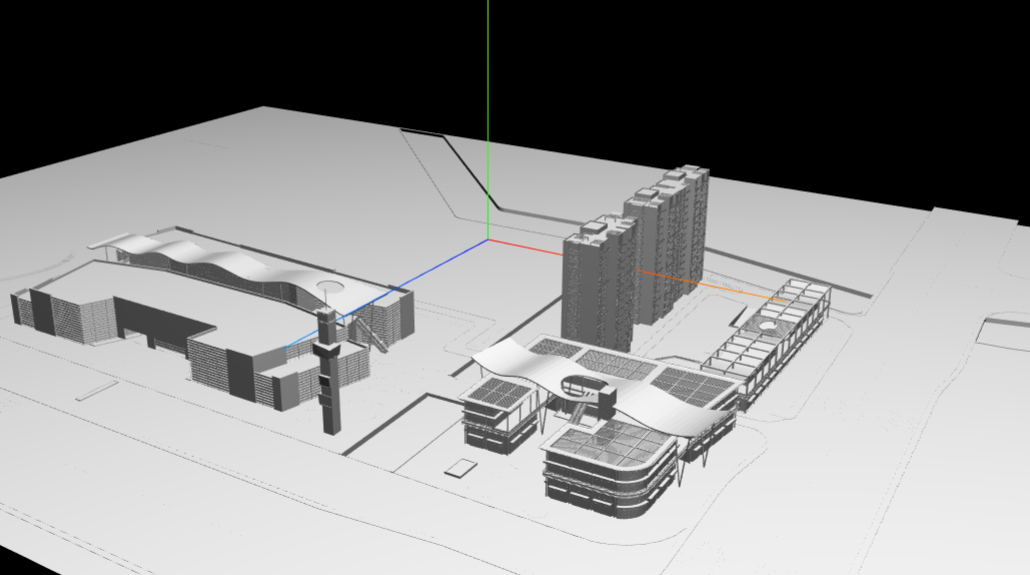
如何将加载后处于偏移位置的模型移动到坐标系原点呢？

原始图
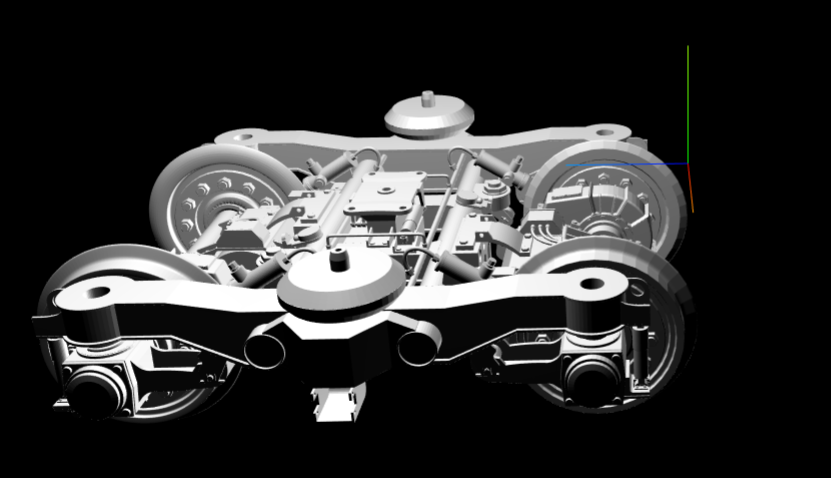
可以看到上图中的模型，虽然模型坐标系和世界坐标系重合，但是模型的原点却位于三维物体的一个角落，看起来不美观。我们起初的办法是通过设置object.children[i].geometry.center()将三维物体的中心移动到模型坐标系原点，但是刚好上图中的模型是单个Mesh构成的三维物体，所以没有发现问题，当使用多Mesh三维模型的时候，上面的方法就会把所有的Mesh移动的模型坐标系中心，使得模型的Mesh混乱，无法显示原来的样子。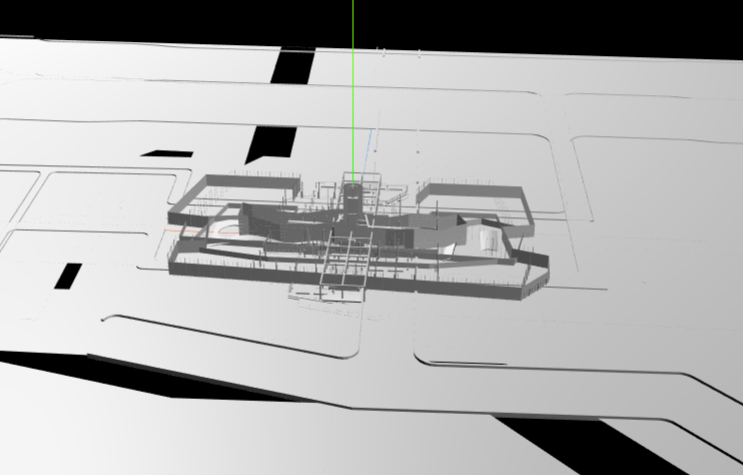
Mesh混乱

为了修复这个问题，想到的解决办法是：计算三维模型AABB包围盒两个对角点的位置坐标相应方向和的均值，得到的均值后，将模型的position设置到这个点，从而达到将三维物体中心放置到坐标系原点的目的。

  1. 加载三维模型

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    objLoader = new THREE.OBJLoader();
    objLoader.setPath('./obj/');
    objLoader.load('a.obj', function (object) {
    oneObj = object;
    object.traverse(function (child) {
        if (child.type === "Mesh") {
            child.geometry.computeBoundingBox();
            child.geometry.verticesNeedUpdate = true;
            child.material.side = THREE.DoubleSide;
            //child.geometry.center(); //设置模型中心点为几何体的中心
        }
    });
    });

  2. 构造AABB包围盒

    1
    box = new THREE.BoxHelper(object);

  3. 计算包围盒任意两个对角点的均值，并移动模型

    1
    2
    3
    4
    5
    var points = box.geometry.attributes.position.array;
    obj_x = (points[0]+points[18])/2;
    obj_y = (points[1]+points[19])/2;
    obj_z = (points[2]+points[20])/2;
    oneObj.position.set(-obj_x,-obj_y,-obj_z); //这是移动模型时要反向移动

moving

这样，就解决了模型便宜的问题，但是模型的大小适配问题还在，我们的思路是：获取到模型表面的距离最远的两个点，然后保证这个距离是小于camera的far-near的，同时这个长度大于far-near x 倍，就相应缩小 n*x倍，n是个放大系数，这里我取值是20。
实现过程如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
    // 获取三维模型表面点的最大距离
    var box3 = new THREE.Box3();
    box3.setFromObject(object);
    var maxLength = box3.getSize(new THREE.Vector3()).length();
    var consult = (camera.far - camera.near) / (20*maxLength);
    //写入场景内
    var currentScale = consult;
    object.scale.set(currentScale,currentScale,currentScale);
``` 

## 实现过程
完整实现过程：

```javascript
        //  objLoader
        objLoader = new THREE.OBJLoader();
        objLoader.setPath('./obj/');
        objLoader.load('a.obj', function (object) {
            oneObj = object;
            object.traverse(function (child) {
                if (child.type === "Mesh") {
                    child.geometry.computeBoundingBox();
                    child.geometry.verticesNeedUpdate = true;
                    child.material.side = THREE.DoubleSide;
                    //child.geometry.center(); //设置模型中心点为几何体的中心
                }
            });
            object.name = "zxj";  //设置模型的名称
            //对模型的大小进行调整
            // object.scale.x =0.001;
            // object.scale.y =0.001;
            // object.scale.z =0.001;
            //object.lookAt(new THREE.Vector3(0,0,0));
            // 加入模型的aabb包围盒
            // 获取三维模型表面点的最大距离
            var box3 = new THREE.Box3();
            box3.setFromObject(object);
            var maxLength = box3.getSize(new THREE.Vector3()).length();
            var consult = (camera.far - camera.near) / (20*maxLength);
            //写入场景内
            var currentScale = consult;
            object.scale.set(currentScale,currentScale,currentScale);
            box = new THREE.BoxHelper(object);
            // box.material.transparents = true;
            // box.material.depthTest = false;
            // box.visible = true;
            var points = box.geometry.attributes.position.array;
            obj_x = (points[0]+points[18])/2;
            obj_y = (points[1]+points[19])/2;
            obj_z = (points[2]+points[20])/2;
            oneObj.position.set(-obj_x,-obj_y,-obj_z);
            //scene.add(box);
            scene.add(object);
        });

裁剪空间(clipspace)

顶点接下来要从观察空间转换到裁剪空间(clip space，也被称为齐次裁剪空间)中，这个用于转换的矩阵叫做裁剪矩阵(clip matrix)，也被称为投影矩阵(projection matrix)。如上面的图所示，裁剪空间是由6个面构成的棱台，它就是webGL中的视锥体，对于这个视锥而言，近平面和远平面分别是近裁剪平面(near clip plane)和远裁剪平面(far clip plane)。裁剪空间的作用就是对存在于视锥体内部的顶点进行渲染，如果不在视锥体内，就裁减掉，不进行渲染。
由此，我们引入一个新的概念：投影矩阵
试想一下，对于这个视锥体而言，如果我们想判断一个点是否在视锥体内部是比较麻烦的，因为视锥体的边界计算就是个复杂的活，那么投影矩阵就是这么一种工具，能够方便的对三维模型的点进行映射，通过结果判断顶点是否位于模型内部。

投影矩阵有两个目的：

  1. 首先是为投影做准备。这是个迷惑点，虽然投影矩阵的名称包含了投影二字，但是它并没有进行真正的投影工作，而是在为投影做准备。真正的投影发生在后面的 齐次除法(homogeneous division) 过程中。而经过投影矩阵的变换后，顶点的 w 分量将会具有特殊的意义。
  2. 其次是对x、y、z分量行进缩放。我们上面讲过直接使用视锥体的6个裁剪平面来进行裁剪会比较麻烦。而经过投影矩阵的缩放后，我们可以直接使用w分量作为一个范围值，如果x、y、z分量都位于这个范围内，就说明该顶点位于裁剪空间内。

在裁剪空间之前，虽然我们使用了齐次坐标来表示点和矢量，但它们的第四个分量都是固定的：点的w分量是1，方向矢量的w分量是0。经过投影矩阵的变换后，我们就会赋予齐次坐标的第4个坐标更加丰富的含义。下面，我们来看一下透视投影使用的投影矩阵具体是什么。

透视投影

fov
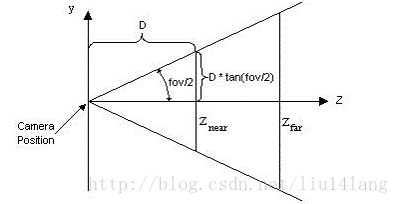
视锥体的意义在于定义了场景中的一块三维空间。所有位于这块空间内的物体将会被渲染，否则就会被剔除或裁剪。我们已经知道，这块区域由6个裁剪平面定义，那么这6个裁剪平面又是怎么决定的呢？它们由Camera组件中的参数和Game视图的横纵比共同决定。
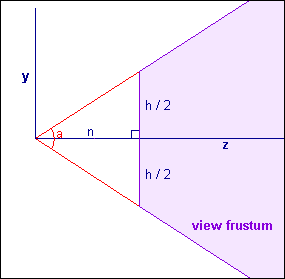
我们可以通过Camera组件的Field of View(简称FOV)属性来改变视锥体竖直方向的张开角度，而Clipping Planes中的Near和Far参数可以控制视锥体的近裁剪平面和远裁剪平面距离摄像机的远近。这样，我们可以求出视锥体近裁剪平面和远裁剪平面的高度，也就是：

$nearClipPaneHeight = 2Neartan(FOV/2)$
$farClipPlaneHeight = 2Fartan(FOV/2)$

现在我们还缺乏横向的信息。这可以通过摄像机的横纵比得到。假设，当前摄像机的横纵比为Aspect，我们定义：

$Aspect = nearClipPlaneWidth/nearClipPlaneHeight$
$Aspect = farClipPlaneWidth/farClipPlaneHeight$

现在，我们可以根据已知的Near、Far、FOV和Aspect的值来确定透视投影的投影矩阵。如下：
投影矩阵
投影矩阵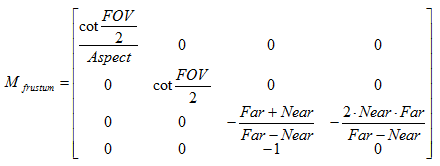
需要注意的是，这里的投影矩阵是建立在WebGL,Unity等对坐标系的假定上面的，也就是说，我们针对的是观察空间为 右手坐标系，使用列矩阵在矩阵右侧进行相乘，且变换后z分量范围将在[-w, w]之间的情况。而在类似DirectX这样的图形接口中，它们希望变换后z分量范围将在[0, w]之间，因此就需要对上面的透视矩阵进行一些更改。
而一个顶点和上述投影矩阵相乘后，可以由观察空间变换到裁剪空间中，结果如下：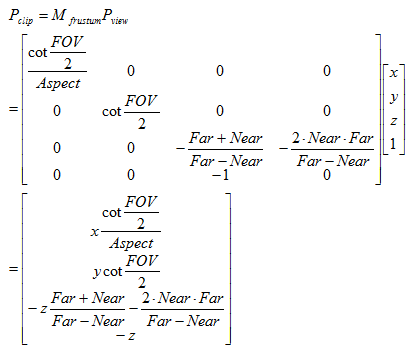
result

从结果可以看出，这个投影矩阵本质就是对x、y和z分量进行了不同程度的缩放(当然，z分量还做了一个平移)，缩放的目的是为了方便裁剪。我们可以注意到，此时顶点的w分量不再是1，而是原先z分量的取反结果。现在，我们就可以按如下不等式来判断一个变换后的顶点是否位于视锥体内。如果一个顶点在视锥体内，那么它变换后的坐标必须满足：

任何不满足上述条件的图元都需要被剔除或者裁剪。

投影矩阵的推导

什么是投影？

在理解投影之前，我们要知道一些知识：计算机屏幕是一个二维图像的展示区域，并不能真正的展示三维的物体，最终的形式还是要以二维平面的形式来展示三维物体，那么也就涉及到了三维物体的二维投影，所以现有的各类图形学库，比如OpenGL，Direct3D 都是研究如何把三维模型转换成二维图像进行渲染方面的工作，这也就是投影的过程。一个简单的例子就是：把3D物体对象投影到2D表面的方法是简单的把没个坐标点的 Z坐标丢弃，对立方体来说，看上去就如下图所示：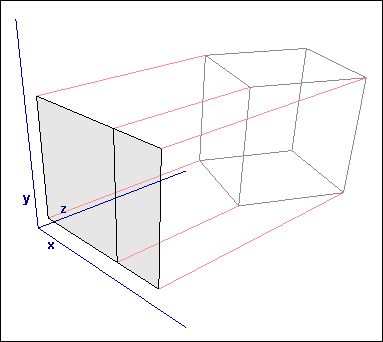
Figure 1: Projection onto the xy plane by discarding z-coordinates.

当然，这种方式是过于简单的，大部分时候不是特别有用。因为大部分不会单纯的舍掉 Z 坐标。而是利用Z坐标来做深度视觉缓冲和可见度方面的工作。
投影公式的作用是将你的几何体变换到一个新的空间体中，这个空间体称为：规范视域体（canonical view volume），规范视域体的精确坐标可能在不同的图形API之间互不相同，但作为讨论起见，把它认为是从(-1, -1, 0)延伸至(1, 1, 1)的盒子，这也是Direct3D中使用的。对于映射到视域体内部的模型而言，它们的x和y坐标被用于映射到屏幕上。这并不代表z坐标是无用的，我们前面提到它通常被深度缓冲用于可见度测试。这就是为什么变换到一个新的空间体中，而不是投影到一个平面上。

正交投影

Orthographic Projection
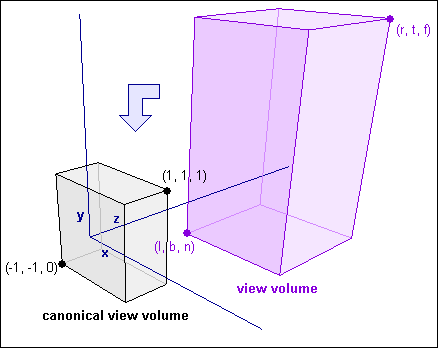
正交投影如上图所示，正如我们看到的，坐标的原点在 规范视域体 的左表面上，而视域体由6个面定义：
left:x = l;
right:x = r;
bottom:y = b;
top:y = t;
near:z = n;
far:z = f
因为视域体和规范视域体都是轴对齐盒子，这种类型的投影没有距离更正。最终的结果是，事实上，很像图1那样每个坐标点只是丢弃了z坐标。正交投影常使用在特定的场景中，比如下图的视图投影：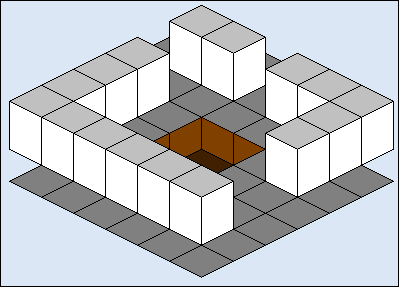
样例
而对于第一人称射击类的游戏，这种正交投影的方式是不可行的。试想一下在不知道任何东西有多远的情况下玩！
所以，我们要弄清楚视域体是如何投影到规范视域体的，最简单的方法可能是3个坐标轴分开考虑，并且计算如何沿着每个坐标轴将点从视域体映射到规范视域体。再来看一下我们前面的视域体的6个面的表示形式：

从x轴的坐标开始变换，对于视域体而言，x的范围是：所以说而我们的目的是将这个视域体变换到$[-1, 1]$:
$l \leq x \leq r$现在，我们的目标是把这个范围缩小到我们期望的$[-1,1]$,所以，第一步：各项减去$l$,这样，左边就变成了0，$0 \leq x-l \leq r-l$ 现在，范围的一段就是0，而我们希望的范围宽度是2个单位，从-1到1，所以把各项乘以$\frac{2}{r-l}$。也就得到了：$0 \leq \frac{2x-2l}{r-l} \leq 2$，下一步各项减去1也就得到了规范视域体的范围$[-1,1]$，

变换一下，可以写成：

最后，把中间项分成两部分使它形如px+q的形式，我们需要把项组织成这种形式这样我们推导的公式就可以简单的转换成矩阵形式：

这个不等式的中间项告诉了我们把x转换到规范视域体的公式：

同样对于y进行坐标变换可以得到：

最后，需要推倒z的变换公式。z的推导有点不同，因为需要把z映射到范围$[0, 1]$而不是$[-1, 1]$，但看上去很相似。
z坐标在视域体中最开始在范围把各项减去$n$，就变成$0 \leq z-n \leq f-n$ 现在剩余要做的就是除以 $f-n$，这样就产生了最终的范围$[0,1]$。和前面相同，注意$f-n$,这样就产生了最终的范围$[0,1]$：

这样便给出了z的变换公式：

现在，可以准备正交投影矩阵了。总结到目前为止的工作，推导了3个投影公式：

写成矩阵形式：

考虑几点: 首先，在可见空间中，摄像机定位在原点并且沿着z轴方向观看。第二，你通常希望你的视野在左右方向上延伸的同样远，并且在z轴的上下方向上也延伸的同样远。如果是这样的情况，那么z轴正好直接穿过你视域体的的中心，所以得到了r = -l并且t = -b。换句话说，你可以把r, l, t和b一起忘掉，简单的把视域体定义为1个宽度w和1个高度h，以及裁剪面f和n。如果你在正交投影矩阵中应用上面说的，那么你将得到这个相当简化的版本：

而其实上面的矩阵可以用两个简单的变换串联替代：平移其次是缩放。如果你思考几何的话这对你是有意义的，因为所有你在正交投影中做的就是从一个轴对齐盒子转向另一个轴对齐盒子；视域体不改变它的形状，只改变它的位置和大小。具体来说：

透视投影

对于透视投影，思想是一样的，但过程略复杂，慢慢再更新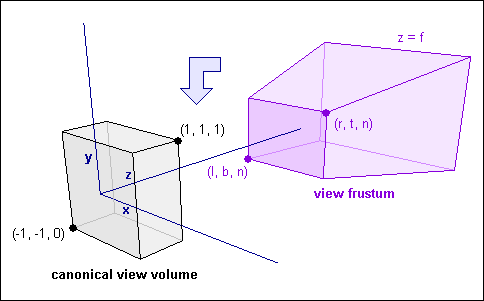
Perspective Projection

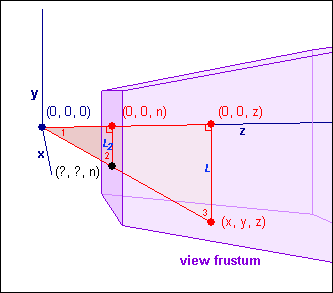
而后得到矩阵表示：

如果你假设视域体是对称的并且中心是z轴(也就是r = -l，t = -b)，你可以简单的用视域体的宽w和高h改写矩阵中的各项：

view frustum

参考：

部分来自如下文章，感谢作者的勤劳付出。
裁剪空间-追风剑情
WebGL
What Is Projection

Donate comment here