认识人工神经网络

写在前面： 或许机器学习这部分内容不应该就这么展开，应该循序渐进，待自己有了深层次了解以后，从基本的回归、分类讲起，但是最后还是选择了边学习边总结的形式，至少能详细记录自己曾经踩过的坑，记录自己的学习路线，也算是个好的形式吧！

---

周末跟北京的兄弟们聚了一波，每次见他们的感觉都特别的不一样，每次见完面后都感觉自己受了很大鼓舞，有无限动力。W哥好像一直都是这么的有激情有干劲儿，YL好像一直这么的能钻研从来不觉得累，而且他们的努力程度远在我认识的其他人之上！一起加油~

---

引言

我相信很多人跟我一样，接触深度学习的最初原因是它很火听起来很厉害，而对于具体是如何实现的，自己根本闹不清……看一些论文、博客的时候都是看到一些类似下图的这样的图片，然后告诉自己：嗯~我大概了解深度学习的概念了。今天我们正儿八经的把它的皮扒开，认真分析它的经脉连通，深入了解什么是神经网络！什么是卷积神经网络，什么是BP神经网络，又是如何延伸到深度学习的！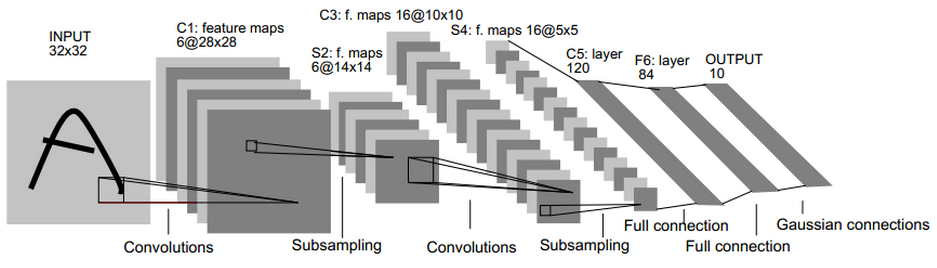

本文我们从神经元讲解到感知器，再到神经网络，带你认识最基本的神经元，然后了解感知器，神经网络是如何工作的！为了保证我的思路不混乱，保证讲解的路线的正确性，我先以自己踩过的坑为带入点，然后依次深入。有关CNN，BP网络，等等我们会在后续文章陆续更新，希望通过几篇文章，理清自己的思路，所机器学习领域的概念有个统筹的认识。

神经网络

好~我们初步解决了一个小问题，那么已经开始上道了，继续分析表象——神经网络，这个词~听起来真的高大上有木有！！第一次听到的时候也是上大学的时候，那时候先进一点的同学都在写神经网络算法，学什么蚁群算法，支持向量机，balabala~~一大堆在当时根本听不懂的名词~那，人总是要进步的，当时不愿意学，研究生再不学就有点耍流氓了~这里我们先介绍什么是神经网络。

神经元

如果你和我一样，是想从0开始，把所有概念全弄懂搭建自己的知识脉络，而不仅仅是关心应用层的东西，我希望你可以看看这部分，看看我这个愚钝的人是如何坑自己的，如果你早已对这些基本概念了解的熟烂于心，建议跳过。
神经元，这个词乍听起来怎么都不能和计算机专业联系在一起，它怎么也得是个生物学相关的东西啊！没错，神经元本就是生物学的概念，第一个人造神经元是1943年由Warren McCulloch和Walter Pitts首次提出的，最早用来作为大脑中“神经网络”的计算模型。如果你不清楚神经元的工作原理，请看下面这个图，神经元有很多个输入端，当输入的信号经过神经元的细胞核处理超过某个阈值后，就把生成的信号向下传递。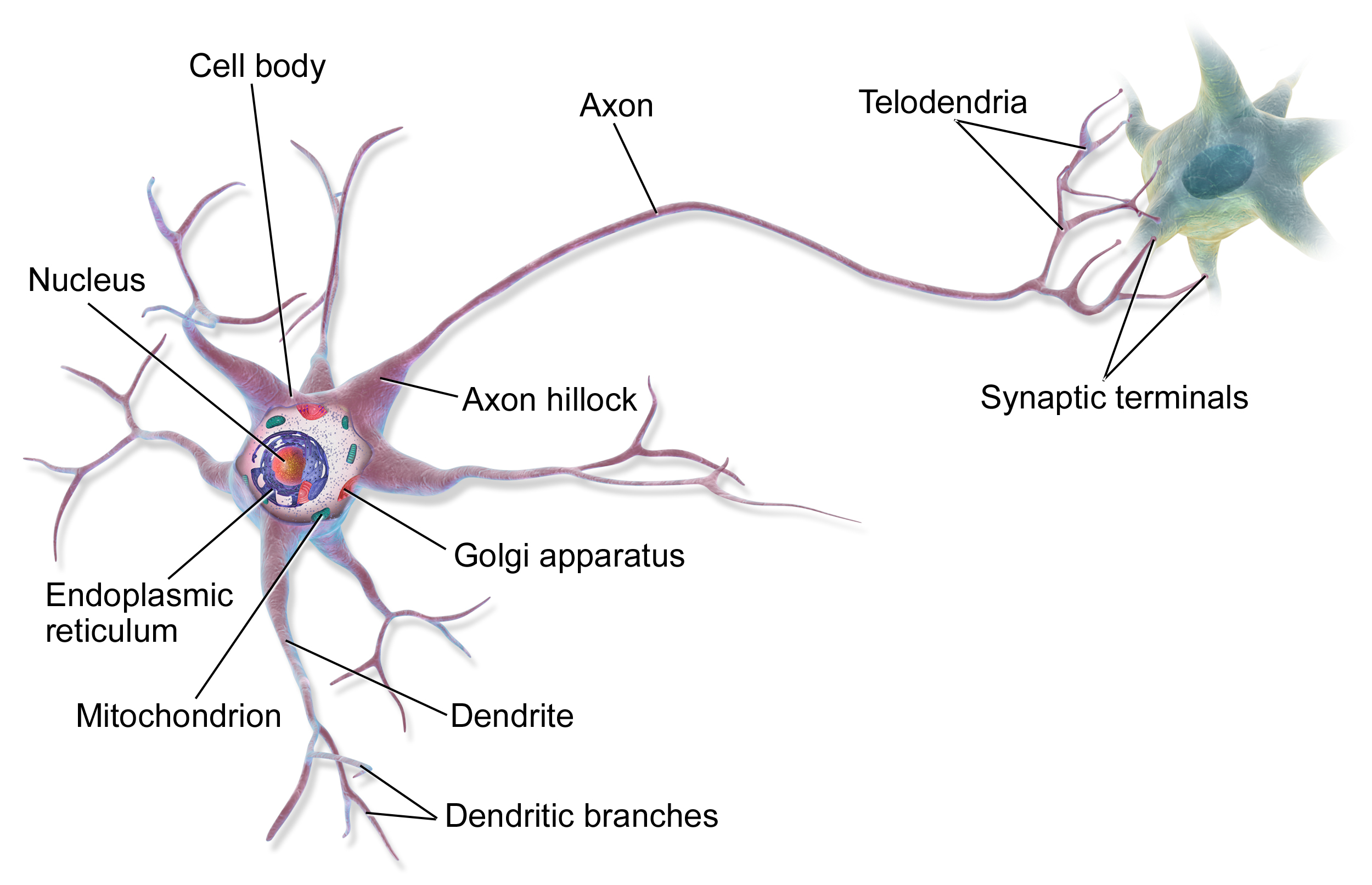

那么知道了真正的神经元的样子，人工神经元实际上就是模拟的生物学中的神经元，如下图所示，左侧的就是输入，中间圆圈就是处理单元，后面的就是输出：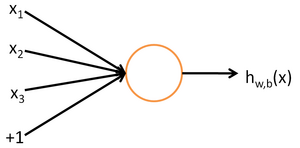

看到这个图，总的来讲我们要有一个概念，这个东西基本表示的是：有多个输入单元，然后将这些输入单元经过某种运算以后得到一个输出。
上图这个神经元的输入值是$x{1},x{2},x{3}$以及截距b这里是$+1$,中间是运算单元，输出是$h{W,b}(x)=f(W^{T}x)=f(\sum^{3}{i=1}W{i}x_{i}+b)$ ,其中函数 $f:\Re \longmapsto \Re$ 被称激活函数。

到这里，其实对于一个非数学或者计算机专业的同学来说已经有点懵了……（其实即使是数学和计算机专业的我，一开始也是懵的……）那么这里这个函数有什么作用呢？我们用一个例子来说明：比如我们有个数据a它的形式是这样的 {$x^{0},1$}，现在我们想通过一个函数能够使得$f(x^{0})=1$那么这个函数$f(x)$就是我们要研究的对象，也就是我们的模型！只不过这里是最简单的一维数据模型，那么让我们把原始输入复杂一点，假设输入是多维数据，（可以用向量来表示）那么就成了$(\boldsymbol x^{(0)},1)$ 也就是说对于这个输入进来的向量，我需要给每个维度的数据配比不同的权重来使得$f(\boldsymbol x^{(0)}) = 1,$;到这里依然很好理解，但是这里还是在讲单一数据，那么对于数据集呢？假设我们有这样的数据集$((\boldsymbol x^{i}),\boldsymbol y^{(i)})$,那我们就无法使用一个神经元来解决问题了，一个不行的话，就多个！那么多个神经元也就组成了我们的神经网络，（多层感知器）。

感知器（Perceptron）

多个神经元构成的组合结构可以成为感知机（感知器）。感知器分为单层感知器和多层感知器。感知器之所以叫感知器原因就是它具备某种感知功能，当我们的网络中具有众多感知各种事物的感知器的时候，也就构成了复杂的神经网络。具有了多重感知能力。这也是感知器与神经网络的关系。

单层感知器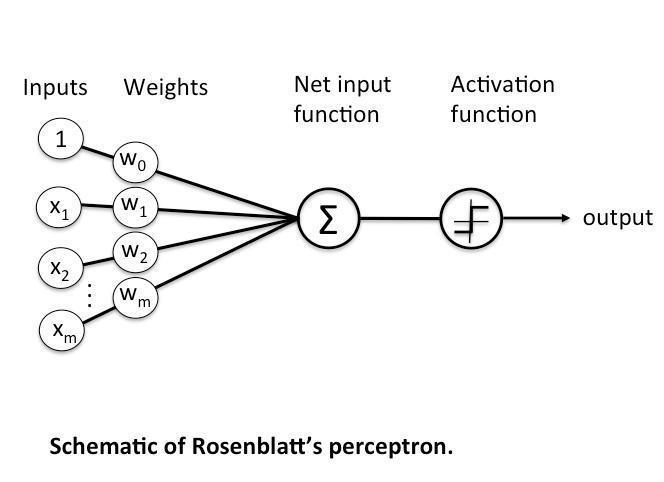

多层感知器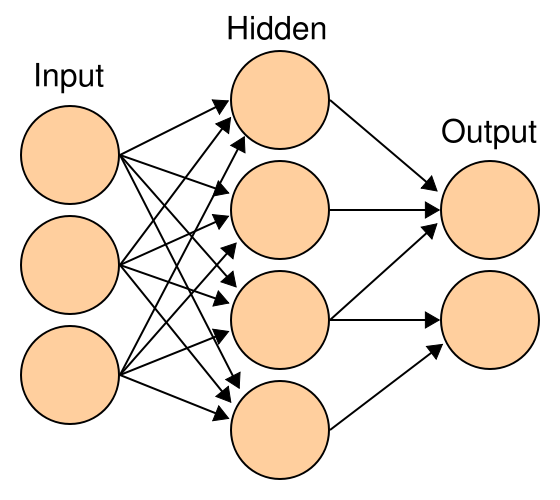

感知器的学习策略

我们需要介绍一下的是，感知机的学习策略，也是我们神经网络中的重点。
首先要明白我们为什么要引入这样一个概念。通过了解上面的神经元和感知器得知，他们的目的是通过一个模型（多层感知器），能够使得样本集$((\boldsymbol x^{i}),\boldsymbol y^{(i)})$ 实现我们的输入$\boldsymbol x^{i}$ 都能和应有的输出$\boldsymbol y^{(i)}$对应上。所以我们的主要目的就是要得到这样的一个模型，对于上面的神经元来说，就是要得到针对各项输入的权重。能够完美匹配我们所有的输入。
好的~到这里，我们基本明确了我们的目标。让我们继续去了解如何解决这个问题
通常我们肯定会遇到这样的情况：我们给一组权重$(w^{i})$和函数$f(x)$它可能只能满足某些输入信号从$x^{(i)}$到$y^{(i)}$的映射，并不能适配所以的样本集。那么如何根据已经正确适配或是适配错误的输出来调整我们的$w^{(i)}$呢？这就引入了我们要讲的重点：学习策略
感知器的学习规则是这样的：学习信号等于神经元期望输出的值与实际的输出值的差。

$$Result = desired_{j} - output_{j} \tag{$1$}$$

$desired{j}$表示期望望的输出，$output{j}$表示实际的输出。$Result$就是误差，然后根据学习信号，就可以对权值进行更新，也就是我们所说的 学习 了。
看到这里不要慌，不要一见到公式就害怕，这里还是很好理解的。只不过把我们前面语言叙述的内容符号化了。
继续，看上面感知器中的图，$W$代表特征向量或者是特征矩阵，$\boldsymbol x$ 表示输入信号（样本集中的样本）。那么我们把上面的公式重新书写一下：

$$output_{j} = f(W^{T}_{j} \cdot X) = sgn(W^{T}_{j} \cdot X) = \begin{cases} 1,& W^{T}_{j}X\geqslant0\\ -1,& W^{T}_{j}X<0\\ \end{cases} \tag{$2$}$$

权值的调整：

$$\vartriangle W_{j} = \eta[desired_{j}-sgn(W^{T}_{j}X)]X \tag{$3$}$$

这个公式右侧的 $\eta$ 表示学习率。权值的调整值 = 学习率$\times$误差$\times$输入信号。当实际的输出与我们期望的输出一致时，也就是$output = desired$ 权值就不需要再调整了。如果以我们的上述中的（5） 式为例，也就是实际的输出值是 1 或者 -1，所以结果可以简化为：

$$\vartriangle W_{j} = \pm 2\eta X \tag{$4$}$$

这就是感知器的学习规则。至于学习率 $\eta$ 它的初始化要符合如下规律：

• 学习率大于零，小于等于１
• 学习率太大，容易造成权值调整不稳定。
• 学习率太小，权值调整太慢，迭代次数太多。
  最初感知器的规则很简单，可以总结为两步：

1. 将权值初始化为0或者较小的随机数。
2. 对每个训练样本：
   • 计算输出值；
   • 更新权值；

输出值就是根据我们早先定义的 激活函数 或者 阶跃函数 预测的类标签$(output = g(z))$,（关于激活函数，我们下面会讲到）并且权值的更新可以写成：

$$w_{j} = w_{j} + \vartriangle w_{j} \tag{$5$}$$

对于每个权值的增量，权值的更新值可以由如下学习规则得到：

$$\vartriangle w_{j} = \eta (target^{(i)} - output^{(i)})x^{(i)}_{j} \tag{6}$$

其中 $\eta$ 表示学习速率（0.0和1.0之间的常数），“target”表示真实标签，“output”表示预测标签。需要注意的是，权值向量内的所有权值同步更新。具体来说，对于一个2维数据集，以如下方式描述更新：

$$\vartriangle w_{0} = \eta (target^{(i)} - output^{(i)}) \tag{7}$$ $$\vartriangle w_{1} = \eta (target^{(i)} - output^{(i)})x^{(i)}_{1} \tag{8}$$ $$\vartriangle w_{2} = \eta (target^{(i)} - output^{(i)})x^{(i)}_{2} \tag{9}$$

设想一下，这种学习规则，如果感知器正确分类，则权值保持不变：

$$\vartriangle w_{(j)} = \eta (-1^{(i)} -- 1^{(i)})x^{(i)}_{j} = 0 \tag{10}$$ $$\vartriangle w_{(j)} = \eta (1^{(i)} - 1^{(i)})x^{(i)}_{j} = 0 \tag{11}$$

但是。如果感知器分类错误，那么权值会向正确“方向”调整：

$$\vartriangle w_{(j)} = \eta (-1^{(i)} - 1^{(i)})x^{(i)}_{j} = \eta (-2)x^{(i)}_{j} \tag{12}$$ $$\vartriangle w_{(j)} = \eta (1^{(i)} + 1^{(i)})x^{(i)}_{j} = \eta (2)x^{(i)}_{j} \tag{13}$$

这就是权值更新的详细过程，需要注意的是，感知器或者神经元分类针对的都是线性可分数据，这样才能保证感知器是收敛的。（关于线性不可分数据，下面会详细介绍）

人工神经网络(ANN)

首先让我们了解一下神经网络的发展史：
1943年，神经科学家和控制论专家Warren McCulloch和逻辑学家Walter Pitts基于数学和阈值逻辑算法创造了一种神经网络计算模型；
1957年，心理学家Frank Rosenblatt创造了模式识别算法感知机，用简单的加减算法实现了两层的计算机学习网络；
1974年，Paul Werbos在博士论文中提出了用误差反向传导来训练人工神经网络有效解决了异或回路问题，使得训练多层神经网络称为可能；
1985年，Rumelhart和McClelland提出了BP网络误差反向传播学习算法；
1998年，以Yann Lecun为首的研究人员实现了一个七层的卷积神经网络LeNet-5识别手写数字；
2006年，以Geoffrey Hinton为代表的加拿大高等研究院附属机构的研究人员开始将人工神经网络/联结主义重新包装为深度学习并进行推广；
2009-2012年，瑞士人工智能实验室IDSIA发展了递归神经网络和深前馈神经网络；
2012年，Geoffrey Hinton组的研究人员在ImageNet2012上夺冠，他们的图像分类效果远远超过了第二名，深度学习热潮由此开始一直持续到现在；

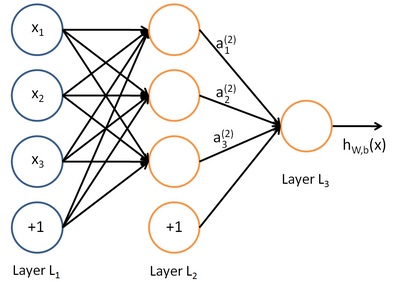
对于人工神经网络，你可以简单的理解成上面的很多神经元或者感知机的结合。

现在，我相信我们大家都很熟悉什么是ANN了，但是在ANN中有什么问题么？仔细回想一下就会发现，我们的ANN都是把上一级的输出当做下一级的输入，中间的处理并不会把一个一街函数升级成二阶函数。激活函数（Activation functions）对于人工神经网络模型去学习、理解非常复杂和非线性的函数来说具有十分重要的作用。它们将非线性特性引入到我们的网络中。其主要目的是将ANN模型中一个节点的输入信号转换成一个输出信号。该输出信号现在被用作堆叠中下一个层的输入。

PS:这里有个问题：为什么多层感知机已经可以解决异或问题了还需要BP神经网络，卷积神经网络？
如果你和我一样有过同样的疑问的话，这里我们可以握个抓，毕竟都是被网上的博客和视频坑过的，推荐还是看本权威的，比如周志华老师的西瓜书《机器学习》。
好，我们回到问题本身，我们有必要有个基本的概念：所谓的神经网络其实就是有众多神经元构成的多层感知器，我们所说的“BP网络”，或者“卷积网络”，就是用BP（Back Propagation）的算法思维，和卷积（Convolution）的算法思维来训练我们的网络（BP主要用来更新权重）从而得到我们的目标多层感知器模型。

顺利入坑

如果看到了这里，恭喜你，已经入坑了，已经有了最基本的概念了，那么让我们继续修行。

什么是异或，线性可分与不可分问题？

首先你要理解什么是线性与非线性。有时候吧，会觉得中文翻译的东西总是缺了一点点的味道，比如说这个线性，英文是 linear ，如果你查一下这个单词，就会知道它其实表示的意思是：“一次的，线性的”；而中文的翻译只保留的“线性”这层含义，去掉了“一次”；这样的结果就是大部分大学老师也很少去强调线性这个词的一次的含义。所以现在你通过这个单词就可以知道，其实线性问题就是一次函数问题，也就是所有的未知量的次数都不大于1。而次数大于1的函数问题，就是非线性问题。这里的异或就属于非线性问题的代表。
在数字逻辑中，异或是对两个运算元的一种逻辑分析类型，符号为XOR或EOR或⊕。与一般的或（OR）不同，当两两数值相同时为否，而数值不同时为真。异或的真值表如下：
我们看下图的异或运算的真值表:

据说在人工神经网络（artificial neural network, ANN）发展初期，由于无法实现对多层神经网络（包括异或逻辑）的训练而造成了一场ANN危机，到最后BP算法的出现，才让训练带有隐藏层的多层神经网络成为可能。因此异或的实现在ANN的发展史是也是具有里程碑意义的。异或之所以重要，是因为它相对于其他逻辑关系，例如与（AND）, 或（OR）等，异或是线性不可分的。如下图：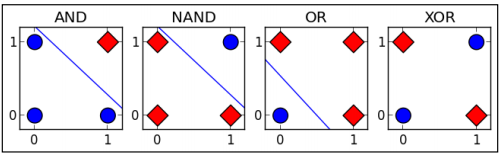

可以知道的是，最后这幅图中的两类点，是不能通过一条直线划分开的。这个直线代表的就是线性分类器，而单层感知机只是各类线性分类器中的一种，所以至此，我们也知道了，为什么线性分类器不能解决异或问题。
机器学习中首先要实现的就是逻辑门。这也是组成数字信号，和程序的基本单元。我们知道逻辑门中有：
与门(AND)，或门(OR)，非门(NOT)，与非门(NAND)，或非门(NOR)，同或门(XNOR)，异或门(XOR)。
在机器学习中，AND（与），NOR（或非）和 OR（或）的组合可以实现XNOR（同或）问题，而（XNOR）同或刚好与XOR相反。
还记的上面的真值表么，表中的相同颜色的点并不能以一条直线分隔开，因为我们的单层感知机也是线性分类器，所以也是无法分开这两者的，所以我们需要设计一种工具是的它可以辅助感知机分离XOR问题，所以到这里我们需要意识到一点，就是不论我们如何设计我们的神经网络，如果不能把 “输出”是“输入”的线性相关函数 这一点改变，我们的网络是永远不能处理异或这类非线性问题的，而输入是输入的次数是无法控制的，权值并不能改变函数的线性相关性，所以只能从输出这一部分入手。所以也就有了在输出层前引入 激活函数（Activation Function） 这个概念。

激活函数 (The Activation Function)

在神经网络中，激活函数的作用是能够给神经网络加入一些非线性因素，使得神经网络可以更好地解决较为复杂的问题。这个Activation Function翻译过来叫做激活函数，一开始的时候我真的以为它是要激活什么东西，比如前面各层神经元或者感知器的输出到达某个值以后才出发什么东西之类的，但是实际的函数结构就是用来将原函数映射到某个区间的工具。然后使得本来是线性的函数可以升次或者降次，从而得到非线性函数以方便处理非线性的复杂分类问题。接下来我们来深度剖析一下激活函数。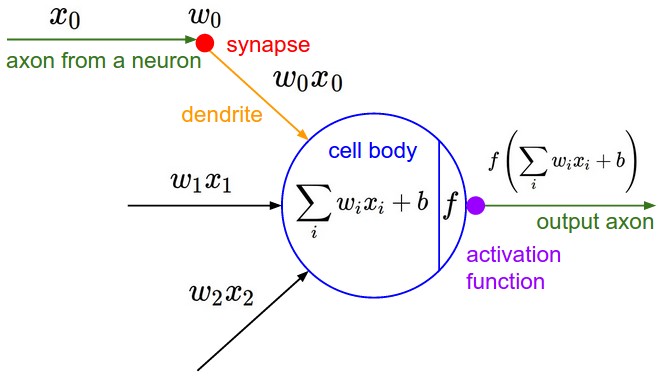

当然这个图，看起来会头大，这大概是毫无疑问的，但等你明白了激活函数的意义，你就会发现它真的简单概括了激活函数的作用。

我们看一下常用的激活函数:

• $\boldsymbol {sigmoid\ funtion}$也叫 $\boldsymbol {Logistic\ function}$ 取值范围(0,1) $$f(z) = \frac{1}{1+e^{-x}}$$
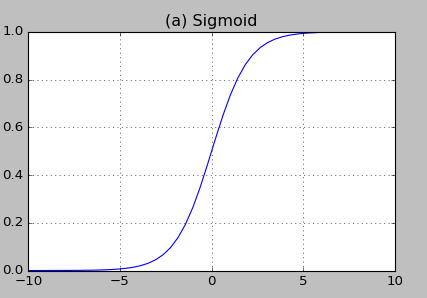
• $\boldsymbol {tanh\ function}$ $$f(z) = tanh(z) = \frac{sinh(x)}{cosh(x)} = \frac{e^{z}-e^{-z}}{e^{z}+e^{-z}}$$ 其中 $$sinh(x) = \frac{e^{x}-e^{-x}}{2}; cosh(x) = \frac{e^{x}+e^{-x}}{2}$$
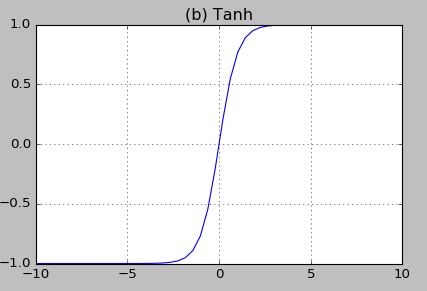
• $\boldsymbol {ReLU\ function (Rectified Linear Unit)}$ $$\phi(x) = max(0, x)$$
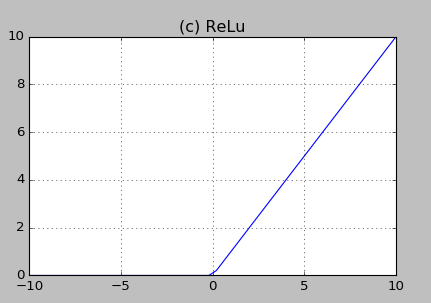
• $\boldsymbol {softmax\ function}$ $$\sigma(z)_{j} = \frac{e^{z}j}{\sum^{K}_{k=1}e^{z}k}$$

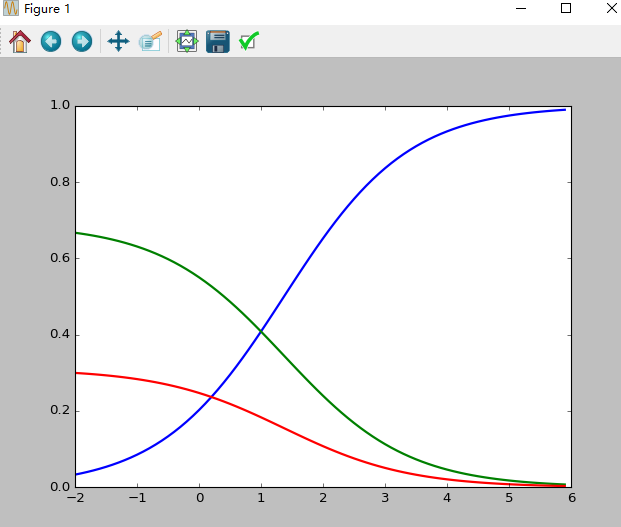
上述函数的用处以及优缺点我们后面会讲到
在实际应用中，我们还会涉及到以下的一些概念：

1. 饱和
   当一个激活函数h(x)满足 $\lim_{x \to +\infty}h’(x) = 0$时我们称之为右饱和。

当一个激活函数h(x)满足$\lim_{x \to -\infty}h’(x) = 0$时我们称之为左饱和。当一个激活函数，既满足左饱和又满足又饱和时，我们称之为饱和。

1. 硬饱和与软饱和
   对任意的$x$，如果存在常数$c$，当$x>c$时恒有$h’(x)=0$则称其为右硬饱和，当$x<c$时恒 有$h’(x)=0$则称其为左硬饱和。若既满足左硬饱和，又满足右硬饱和，则称这种激活函数为硬饱和。但如果只有在极限状态下偏导数等于0的函数，称之为软饱和。

参考

1. 激活函数的作用
2. 神经网络
3. 感知器

   代码实现

   用Python实现感知器规则

题目：假设平面坐标系上有几个点(２,3), (4,５), (５,３)这三个点的标签为1，(０,1)，(1,1)这两个点的标签为-1,构建神经网络来分类

思路：

• 构造神经元-单层感知器，有三个输入节点 (1,2,3),(1,4,5), (1,1,1)
• 对应的数据标签为(1,1,-1)
• 初始化权重值 $w{0}$,$w{1}$,$w_{2}$为-1到1之间的随机数
• 学习率设置为0.11
• 激活函数为$Sign$函数

import numpy as np
import matplotlib.pyplot as plt

n = 0            #迭代次数
lr = 0.11        #学习速率

# 输入数据
X = np.array([[1,1,2,3],
              [1,1,4,5],
              [1,1,1,1],
              [1,1,5,3],
              [1,1,0,1]])
# 标签
Y = np.array([1,1,-1,1,-1])

# 权重初始化，取值范围-1到1
W = (np.random.random(X.shape[1])-0.5)*2
print('初始化权值：',W)

def get_show():
    # 所有样本的坐标
    all_x = X[:, 2]
    all_y = X[:, 3]
    # 额外注释标签为-1的负样本的坐标
    all_negative_x = [1, 0]
    all_negative_y = [1, 1]
    # 计算分界线斜率与截距
    k = -W[2] / W[3]
    b = -(W[0] +W[1])/ W[3]
    print('斜率 k=', k)
    print('截距 b=', b)
    print('分割线函数：y = ', k,'x +(', b, ')')
    xdata = np.linspace(0, 5)
    plt.figure()
    plt.plot(xdata,xdata*k+b,'r')
    plt.plot(all_x, all_y,'bo')
    plt.plot(all_negative_x, all_negative_y, 'yo')
    plt.show()

#更新权值函数
def get_update():
    global X,Y,W,lr,n
    n += 1
    #新输出：X与W的转置相乘，得到的结果再由阶跃函数处理，得到新输出
    new_output = np.sign(np.dot(X,W.T))
    #调整权重: 新权重 = 旧权重 + 改变权重
    new_W = W + lr*((Y-new_output.T).dot(X))/int(X.shape[0])
    W = new_W

def main():
    for _ in range(100):
        get_update()
        print('第',n,'次改变后的权重：',W)
        new_output = np.sign(np.dot(X, W.T))
        if (new_output == Y.T).all():
            print("迭代次数：", n)
            break
    get_show()

if __name__ == "__main__":
    main()

输出结果为：

初始化权值： [ 0.71761357 -0.01222642  0.86193314  0.16775246]
第 1 次改变后的权重： [ 0.62961357 -0.10022642  0.81793314  0.07975246]
第 2 次改变后的权重： [ 0.54161357 -0.18822642  0.77393314 -0.00824754]
第 3 次改变后的权重： [ 0.45361357 -0.27622642  0.72993314 -0.09624754]
第 4 次改变后的权重： [ 0.36561357 -0.36422642  0.68593314 -0.18424754]
第 5 次改变后的权重： [ 0.32161357 -0.40822642  0.64193314 -0.22824754]
第 6 次改变后的权重： [ 0.27761357 -0.45222642  0.59793314 -0.27224754]
第 7 次改变后的权重： [ 0.23361357 -0.49622642  0.55393314 -0.31624754]
第 8 次改变后的权重： [ 0.27761357 -0.45222642  0.64193314 -0.18424754]
第 9 次改变后的权重： [ 0.23361357 -0.49622642  0.59793314 -0.22824754]
第 10 次改变后的权重： [ 0.18961357 -0.54022642  0.55393314 -0.27224754]
第 11 次改变后的权重： [ 0.23361357 -0.49622642  0.64193314 -0.14024754]
第 12 次改变后的权重： [ 0.18961357 -0.54022642  0.59793314 -0.18424754]
第 13 次改变后的权重： [ 0.14561357 -0.58422642  0.55393314 -0.22824754]
第 14 次改变后的权重： [ 0.18961357 -0.54022642  0.64193314 -0.09624754]
第 15 次改变后的权重： [ 0.14561357 -0.58422642  0.59793314 -0.14024754]
第 16 次改变后的权重： [ 0.10161357 -0.62822642  0.55393314 -0.18424754]
迭代次数： 16
斜率 k= 3.0064615780789095
截距 b= -2.8581812250111303
分割线函数：y =  3.0064615780789095 x +( -2.8581812250111303 )

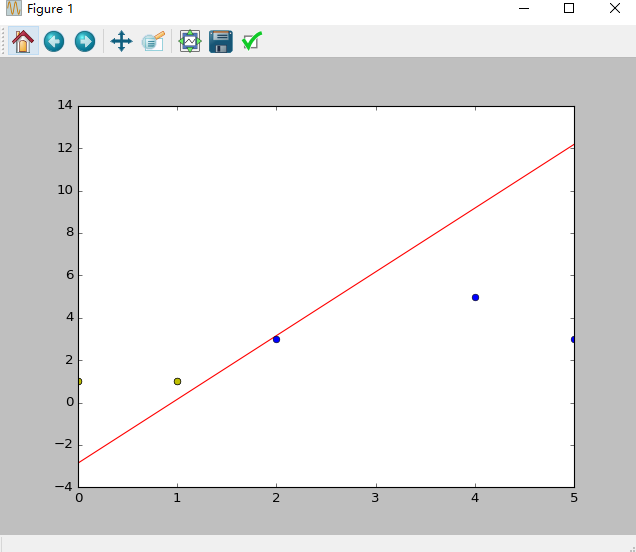
异或问题-增加非线性项

异或问题不是线性可以求解的，解决方式有增加非线性项。
问题例如：平面上的点(0,0), (1,1) 对应的数据标签为-1，平面上的点(0,1), (1,0) 对应的数据标签为 1，构造单层感知器以区分两类数据点。

'''
异或问题的解决方式有：增加非线性项:
     输入x1,x2；
     增加x1^2,x1*x2,x2^2
'''

import numpy as np
import matplotlib.pyplot as plt

n = 0            #迭代次数
lr = 0.11        #学习速率

#输入数据分别:偏置值,x1,x2,x1^2,x1*x2,x2^2
X = np.array([[1,0,0,0,0,0],
              [1,0,1,0,0,1],
              [1,1,0,1,0,0],
              [1,1,1,1,1,1]])

#标签
Y = np.array([-1,1,1,-1])

# 权重初始化，取值范围-1到1
W = (np.random.random(X.shape[1])-0.5)*2
print('初始化权值：',W)

def get_show():
    # 正样本
    x1 = [0, 1]
    y1 = [1, 0]
    # 负样本
    x2 = [0,1]
    y2 = [0,1]
    xdata = np.linspace(-1, 2)
    plt.figure()
    plt.plot(xdata, get_line(xdata,1), 'r')
    plt.plot(xdata, get_line(xdata,2), 'r')
    plt.plot(x1, y1, 'bo')
    plt.plot(x2, y2, 'yo')
    plt.show()

def get_line(x,root):
    a = W[5]
    b = W[2] + x*W[4]
    c = W[0] + x*W[1] + x*x*W[3]
    if root == 1:
        return (-b+np.sqrt(b*b-4*a*c))/(2*a)
    if root == 2:
        return (-b-np.sqrt(b*b-4*a*c))/(2*a)

#更新权值函数
def get_update():
    global X,Y,W,lr,n
    n += 1
    #新输出：X与W的转置相乘，得到的结果再由阶跃函数处理，得到新输出
    new_output = np.dot(X,W.T)
    #调整权重: 新权重 = 旧权重 + 改变权重
    new_W = W + lr*((Y-new_output.T).dot(X))/int(X.shape[0])
    W = new_W

def main():
    for _ in range(10000):
        get_update()
    get_show()
    last_output = np.dot(X,W.T)
    print('最后逼近值：',last_output)

if __name__ == "__main__":
    main()

输出结果：

初始化权值： [ 0.53493581  0.84054602 -0.49422516  0.86122222 -0.84342568 -0.57384193]
最后逼近值： [-1.  1.  1. -1.]

图像：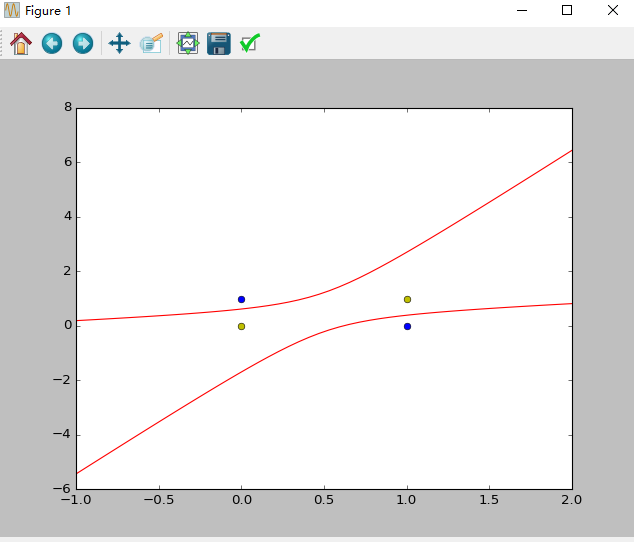

Python实现简单的感知器学习规则以分类鸢尾花数据集分类。

我们将从UCI Machine Learning Repository载入鸢尾花数据集，并只关注Setosa 和Versicolor两种花。此外，为了可视化，我们将只使用两种特性：萼片长度（sepal length ）和花片长度（petal length）。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from mlxtend.plotting import plot_decision_regions

class Perceptron(object):
  def __init__(self, eta=0.01, epochs=50):
    self.eta = eta
    self.epochs = epochs

  def train(self, X, y):
    self.w_ = np.zeros(1 + X.shape[1])
    self.errors_ = []
    for _ in range(self.epochs):
      errors = 0
      for xi, target in zip(X, y):
        update = self.eta * (target - self.predict(xi))
        self.w_[1:] +=  update * xi
        self.w_[0] +=  update
        errors += int(update != 0.0)
      self.errors_.append(errors)
    return self

  def net_input(self, X):
    return np.dot(X, self.w_[1:]) + self.w_[0]

  def predict(self, X):
    return np.where(self.net_input(X) >= 0.0, 1, -1)


df = pd.read_csv('https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data', header=None)

# setosa and versicolor
y = df.iloc[0:100, 4].values
y = np.where(y == 'Iris-setosa', -1, 1)

# sepal length and petal length
X = df.iloc[0:100, [0,2]].values


ppn = Perceptron(epochs=10, eta=0.1)
ppn.train(X, y)
print('Weights: %s' % ppn.w_)

plot_decision_regions(X, y, clf=ppn)
plt.title('Perceptron')
plt.xlabel('sepal length [cm]')
plt.ylabel('petal length [cm]')
plt.show()

plt.plot(range(1, len(ppn.errors_)+1), ppn.errors_, marker='o')
plt.xlabel('Iterations')
plt.ylabel('Missclassifications')
plt.show()

输出：
Weights: [-0.4 -0.68 1.82]
图像：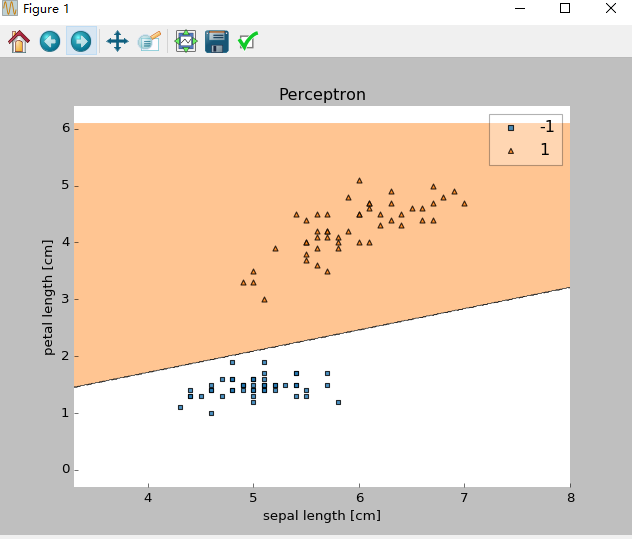

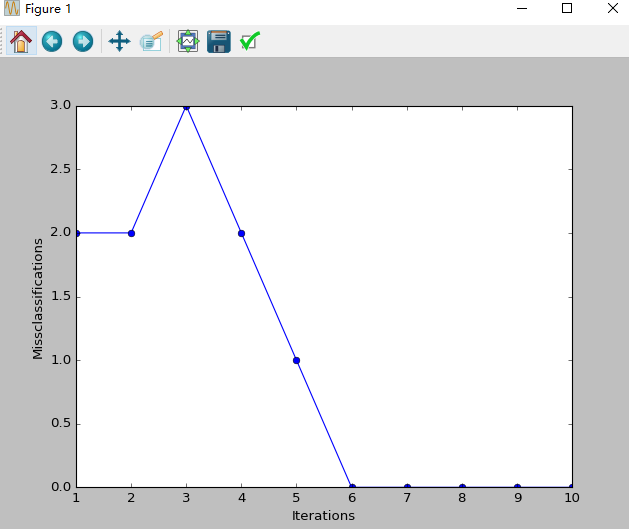
感知器存在的问题

• 尽管感知器完美地分辨出两种鸢尾花类，但收敛是感知器的最大问题之一。 Frank Rosenblatt在数学上证明了当两个类可由线性超平面分离时，感知器的学习规则收敛，但当类无法由线性分类器完美分离时，问题就出现了。为了说明这个问题，我们将使用鸢尾花数据集中两个不同的类和特性。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from mlxtend.plotting import plot_decision_regions

class Perceptron(object):
  def __init__(self, eta=0.01, epochs=50):
    self.eta = eta
    self.epochs = epochs

  def train(self, X, y):
    self.w_ = np.zeros(1 + X.shape[1])
    self.errors_ = []
    for _ in range(self.epochs):
      errors = 0
      for xi, target in zip(X, y):
        update = self.eta * (target - self.predict(xi))
        self.w_[1:] +=  update * xi
        self.w_[0] +=  update
        errors += int(update != 0.0)
      self.errors_.append(errors)
    return self

  def net_input(self, X):
    return np.dot(X, self.w_[1:]) + self.w_[0]

  def predict(self, X):
    return np.where(self.net_input(X) >= 0.0, 1, -1)


df = pd.read_csv('https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data', header=None)

# versicolor and virginica
y2 = df.iloc[50:150, 4].values
y2 = np.where(y2 == 'Iris-virginica', -1, 1)

# sepal width and petal width
X2 = df.iloc[50:150, [1,3]].values

ppn = Perceptron(epochs=25, eta=0.01)
ppn.train(X2, y2)

plot_decision_regions(X2, y2, clf=ppn)
plt.show()

plt.plot(range(1, len(ppn.errors_)+1), ppn.errors_, marker='o')
plt.xlabel('Iterations')
plt.ylabel('Missclassifications')
plt.show()
print('Total number of misclassifications: %d of 100' % (y2 != ppn.predict(X2)).sum())

输出：
Total number of misclassifications: 43 of 100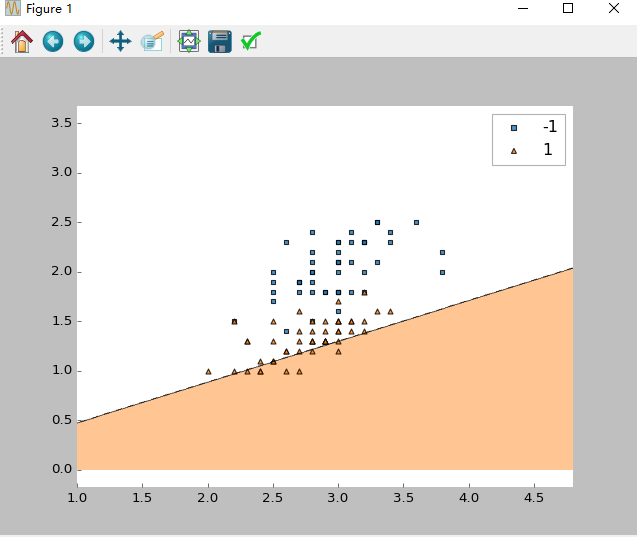

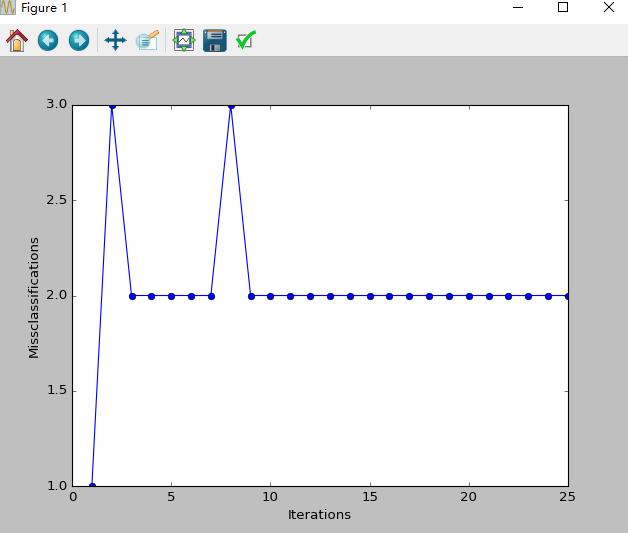
• 在较低的学习率情形下，因为一个或多个样本在每一次迭代总是无法被分类造成学习规则不停更新权值，最终，感知器还是无法找到一个好的决策边界。
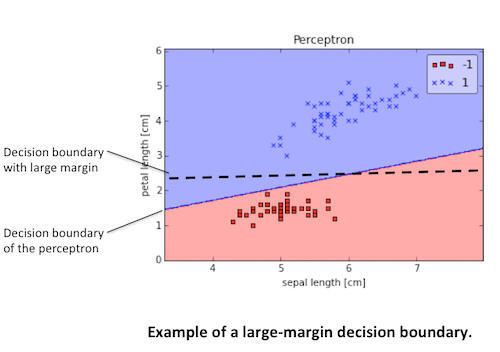
• 感知器算法的另一个缺陷是，一旦所有样本均被正确分类，它就会停止更新权值，这看起来有些矛盾。直觉告诉我们，具有大间隔的决策面（如下图中虚线所示）比感知器的决策面具有更好的分类误差。但是诸如“Support Vector Machines”之类的大间隔分类器不在本次讨论范围。