MachineLearning之SVM

了解SVM (Support Vector Machine—支持向量机)

线性可分数据

SVM(Support Vector Machine)是支持向量机，是常见的一种判别方法。在机器学习领域，是一个有监督的学习模型（通过改进，当数据未被标记时，不能进行监督式学习，需要用非监督式学习，它会尝试找出数据到簇的自然聚类，并将新数据映射到这些已形成的簇。将支持向量机改进的聚类算法被称为支持向量聚类），通常用来进行模式识别、分类以及回归分析。

SVM的目的

通过上一章的KNN，我们已经了解到，它可以对数据进行分类处理了：思想就是通过计算每个元素与待分类元素的距离来进行判断。这样做的缺点是需要大量的计算和存储（因为需要计算每个点到待测点的距离）;而SVM就是为了解决这样的问题而诞生的.如下图: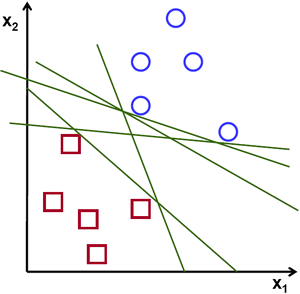

考虑这种情况：我们有一条线，它的函数形式为：$f(x) = ax{1}+bx{2}+c$（x为测试数据）, 通过这条线，可以将数据划分成两个部分。（如上图中的线），当我们新得到一个测试数据$X$的时候，只需要将$X$代入到函数$f(x)$中进行计算。如果$f(x) > 0$ 这个测试样本就属于蓝色的类别，否则它属于红色的类别。我们把这个函数对应的直线叫做：决策边界(Decision Boundary)，这种判断的形式非常简单，而且节省内存。
像这类我们可以通过使用一条直线（或者高维的超平面）将其分为两部分的数据，我们称其为：线性可分数据。
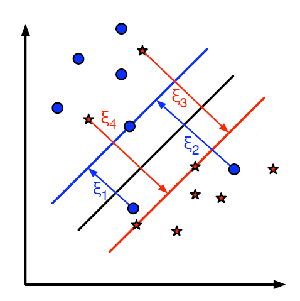
所以，在上面的图片中我们可以找到很多这样的直线，那么，采用哪一条直线是合理的呢？答案是：距离两侧的点越远越好，这样是最好的分类边界(目的是对抗噪声)；因此，SVM所做的就是找到一条直线（或超平面），最大化它与训练样本的距离。类似图像中通过中心的粗线。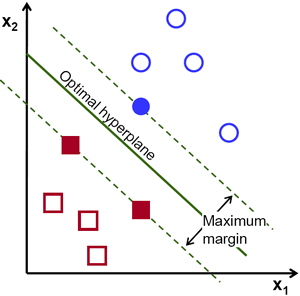

为了找到这个决策边界，我们需要一些训练数据，事实上，我们仅需要两个类别相邻处的一部分数据就可以了。在我们的上图中的例子中，两个类别边界的的临近数据我们选择的分别是两个红色的方块和一个蓝色的圆圈。我们把他们叫做：支持向量（Support Vectors），通过他们的线（虚线）叫做：支持平面(Support Planes)。通过他们足以发现我们需要找到的决策边界。
举个例子：蓝色数据是通过$w^{T}x+b{0}>1$来表示的，同时红色数据是由$w^{T}x+b{0}<-1$来表示的。（$w$是权重向量$(w=[w{1},w={2},w{3},…,w{n}])$）同时$x$是特征向量$(x=[x{1},x{2},x{3},…,x{n}])$。$b{0}$ 是 bias偏置项。决策边界的表示为：$w^{T}x+b{0}=0$ 。从支持向量到决策边界的最小距离由下式给出$distance{support \, vectors}=\frac{1}{||w||}$，margin是这个边界距离两倍，我们需要的是最大化的margin。如图中的例子，我们需要找到了一个最小化的function:$L(w,b{0})$它的公式构成如下：

$$\min_{w,b_{0}}L(w,b_{0} = \frac{1}{2}||w||^{2})subject\ to\ t_{i}(w^{T}x+b_{0})\geqslant1\forall{i}$$

其中$t{i}$是每一个类的标签label，$t{i}\in {-1,1}$

对于上述公式的解读

上面讲到的SVM的核心就是：使得超平面与和它距离最近的点的距离最大化。这个距离，我们就可以理解成几何距离；很好理解，例如对于上图中的二维平面，就是点到直线的距离（这里直线就是超平面）；对于三维空间，就是点到平面的距离；以及高维空间的点到超平面的距离；计算公式都是相同的。在SVM中，把这个几何距离叫做：几何间隔。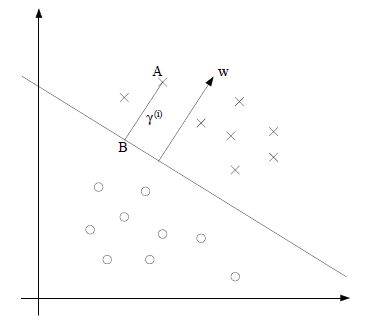

例如，在上图的二维空间中，点A到分隔超平面（直线）的距离即为线段AB的长度。几何间隔的计算公式如下：（其中$y^{i}$表示数据点的类别标签，$w,b$分别是超平面$w^{T}x+b=0$的参数）

$$\gamma ^{(i)}=y^{(i)}((\frac{w}{||w||})^{T}x^{(i)}+\frac{b}{||w||})$$

需要注意的是这里分子上是没有绝对值符号的。而我们通常求的距离公式中是有绝对值符号的。（这里后续会详细说明）

---

距离公式的推导过程：

我们知道对于二维平面上的点到直线的距离公式为:

$$d=\frac{|Ax+By+C|}{\sqrt{A^{2}+B^{2}}}$$

PS：这个公式的推导过程如下：
运用三角形面积相等法则: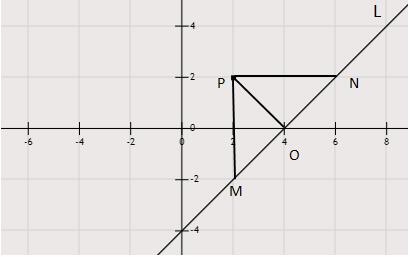

我们已知$P(x{0},y{0})$,直线方程为：$Ax+By+C=0$。三角形$\triangle PMN$的面积等于$\frac{PM \bullet PN} {2} = \frac{MN \bullet PO} {2}$所以，我们把$P$点坐标$(x{0},y{0})$中的$x{0}$带入到直线方程中，可以得到直线上横坐标为$x{0}$的点的纵坐标，然后用这个坐标减去$P$点的纵坐标，再取模就可以得到$PM$的长度。同理可以得到PN的长度。

$$\because |PM| = |\frac{Ax_{0}+By_{0}+C}{B}|$$ $$|PN| = |\frac{Ax_{0}+By_{0}+C}{A}|$$ $$\therefore |PO| = \frac{|PM|*|PN|}{\sqrt{|PM|^{2}+|PN|^{2}}}$$

对于三维空间中的距离公式:

$$d=\frac{|Ax+By+Cz+D|}{\sqrt{A^{2}+B^{2}+C_{2}}}$$

高维空间：

$$d=\frac{|A_{1}x_{1}+A_{2}x_{2}+...A_{n}x_{n}|}{\sqrt{A_{1}^{2}+A_{2}^{2}+...+A_{n}^{2}}}$$

所以，以向量的形式来书写这个公式，高维空间的几何距离为：

$$d = \frac{|w^{T}x+b|}{||w||}$$

---

所以通过上面的推导，我们可以得知高维空间的几何间隔就是这样的计算方式这里的$y^{(i)}$是$x^{(i)}$对应的标签类，属于[-1,+1]与函数间隔做乘后可以判断出是否分类正确：

$$\gamma ^{(i)}=y^{(i)}((\frac{w}{||w||})^{T}x^{(i)}+\frac{b}{||w||})$$

可以看到这个公式与上面的不同是后者是没有绝对值符号的，
而SVM中的函数间隔就是指的上式中的分子：$y^{(i)}(w^{T}x+b)$ 也就是未归一化之前的距离。并且函数间隔是带正负号的，也就是表示样本集是属于正样本还是负样本，通过函数间隔是可以得出的。这个公式可以认作是任意样本点到超平面的距离。
更要注意的一点是：$y^{(i)}$是与后面的同号的，这样才能保证分类是正确的。才能使得乘积是大于0的。
下图中，在超平面上侧的数据集带入到超平面公式中是 $w^{T}x^{(i)}+b < 0$，在超平面下侧的数据集带入到超平面公式中 $w^{T}x^{(i)}+b > 0$，这样的话，$y^{(i)}$ 的值就是要保证与前面的公式同号，上半部分的$y^{(i)}$值应该是负的，下半部分的$y^{(i)}$值应该是正的。（这里$y^{(i)}$怎么确定的，到现在也不明白。）

2018.5.9更新：[$y^{(i)}$标签的由来，以及实例介绍]
我们考虑以下形式的n点测试集：$(\vec{x{1}},y{1}),…,(\vec{x{n}},y{n})$其中$y{i}$是1或者-1，表明点$\vec{x{i}}$中每个都是一个$p$ 维实向量。我们想要得到的是将$y{i}=1$的点集与$y{i}=-1$的点集分开的“最大间隔超平面”，使得超平面与最近的点$\vec{x_{i}}$之间的距离最大化。任何超平面都可以写作满足以下方程的点集$\vec{x}$。

$$\vec{w} \cdot \vec{x} -b=0$$

公式很好理解：实际就是三维空间中平面表示法的一般式$Ax+By+Cz+D=0$;因为$A,B,C$可以构成一个平面的法向量，所以这里的$\vec{w}$也是法向量，$\frac{b}{||\vec{w}||}$决定从原点沿着法向量方向到差平面的偏移量。

实际：这个$w^{T}x^{(i)}+b$就是一个分类器，而分类器不过就是二维平面中的直线，三维空间中的平面，高维空间中的超平面罢了。

---

关于$y(i)$

$y(i)$是样本数据的标签，$y(i)\in {-1,1}$

$$\begin{cases} (w \cdot x_{i})+b \geqslant 1,& y_{i}=+1\\ (w \cdot x_{i})+b \leqslant 1,& y_{i}=-1 \end{cases}$$

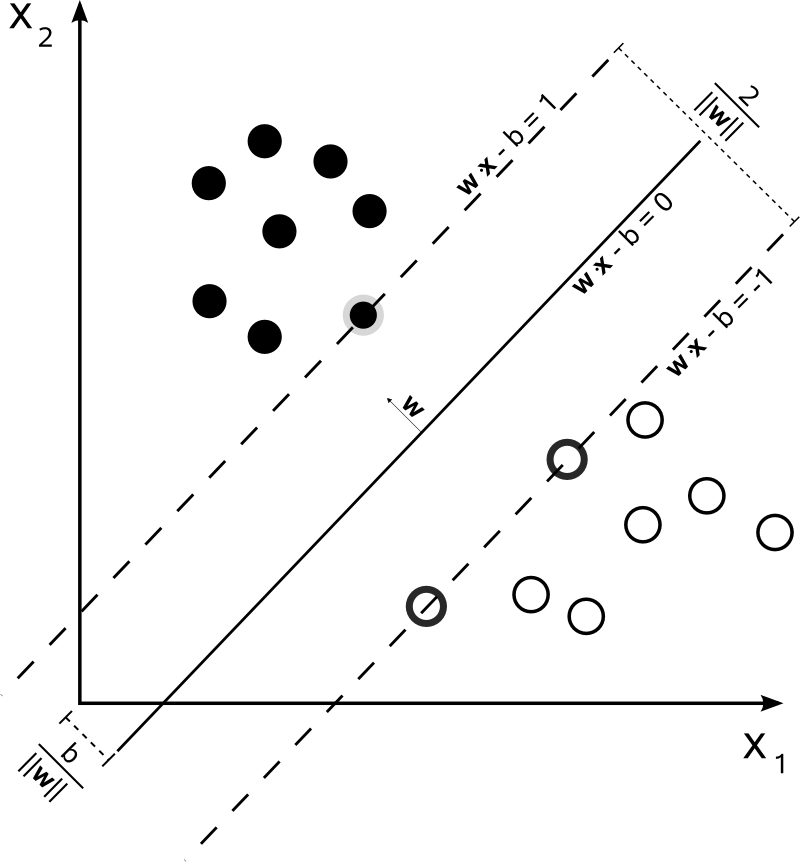
如上面的图像所示：离超平面最近的点到最优超平面的距离就是$margin$，我们要优化的，就是使得这个$margin$最大化。又因为最大间隔超平面（也就是最优超平面）位于两个数据集分割平面的中间，而分割两个数据集的平面是无数多的，（可以称为超平面簇）而超平面簇的两个最边缘的平面表达式为：

$$\begin{cases} \vec{w}\cdot\vec{x}-b=1 \\ \vec{W}\cdot\vec{x}-b=-1 \end{cases}$$

不难得到两个超平面的距离就是$\frac{2}{||\vec{w}||}$，因此我们需要最大化间隔，就是最小化$||\vec{w}||$。同时为了使得样本数据点都在超平面的间隔以外，我们就有了上面的公式：

$$\begin{cases} (w \cdot x_{i})+b \geqslant 1,& y_{i}=+1\\ (w \cdot x_{i})+b \leqslant 1,& y_{i}=-1 \end{cases}$$

最大间隔超平面完全是由最靠近它的那些 ${\displaystyle {\vec {x}}{i}}$ 确定的。这些 ${\displaystyle {\vec {x}}{i}}$ 叫做支持向量。

对于线性不可分数据（待续）