MachineLearning之KNN

发表于 | 分类于

KNN (k-Nearest Neighbour) K临近算法

kNN是可用于监督学习的最简单的分类算法之一。它的思想是：在特征空间中搜索最匹配的测试数据。
所谓K临近，就是k个最近的邻居的意思，说的是每个样本都可以用它最接近的k个邻居来代表。kNN算法的核心思想是：如果一个样本在特征空间中的k个最相邻的样本中的大多数属于某一个类别，则该样本也属于这个类别，并具有这个类别上样本的特性。该方法在确定分类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。 kNN方法在类别决策时，只与极少量的相邻样本有关。由于kNN方法主要靠周围有限的邻近的样本，而不是靠判别类域的方法来确定所属类别的，因此对于类域的交叉或重叠较多的待分样本集来说，kNN方法较其他方法更为适合。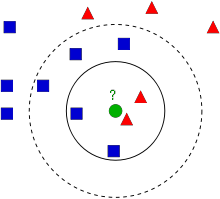

像上图中的例子，红色的三角和蓝色的方块是已经存在的图形，从我们人类的分类角度来看，把方块看作一类，把三角看作一类，是合理的办法，但是计算机如何去实现这样的分类呢？比如我们现在想知道这个新加入的绿色的圆圈属于什么类别？KNN的思想如下：我们寻找距离圆圈最近的K个特征，比如K=3，我们找到了两个三角，一个方块，我们认定它有2/3的概率是三角，所以归为”三角”类，又如K=7，距离圆圈最近的7个元素中，有5个方块，2个三角，所以有5/7的概率是方块，所以它被归类到方块。

KNN算法的实现步骤：

  1. 计算距离
  2. 选择距离最小的k个点
  3. 排序

改进：

在使用KNN的过程中难免会遇到如下情况：当计算需要分类的点与其他点的距离时，当给定一个K值，发现距离它最近的两个类中的元素数量是一样的，这样就有了后续的改进算法。

Python代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
import cv2
import numpy as np
import matplotlib.pyplot as plt
# Feature set containing (x,y) values of 25 known/training data
# 10个特征数据，每个数据都是由一个坐标构成，每个数都是0~100之间的随机数
# 特征数据矩阵为10行，2列 ：[10,2]
trainData = np.random.randint(0,100,(10,2)).astype(np.float32)
# Labels each one either Red or Blue with numbers 0 and 1
# 给每个数据标定label
responses = np.random.randint(0,2,(10,1)).astype(np.float32)
# Take Red families and plot them
# 让label = 0的数据为red三角
red = trainData[responses.ravel()==0]
plt.scatter(red[:,0],red[:,1],80,'r','^')
# Take Blue families and plot them
# 让label = 1的数据为blue的方块
blue = trainData[responses.ravel()==1]
plt.scatter(blue[:,0],blue[:,1],80,'b','s')
# 新加入的绿色圆圈
newcomer = np.random.randint(0,100,(1,2)).astype(np.float32)
plt.scatter(newcomer[:,0],newcomer[:,1],80,'g','o')
knn = cv2.ml.KNearest_create()
knn.train(trainData, cv2.ml.ROW_SAMPLE, responses)
ret, results, neighbours ,dist = knn.findNearest(newcomer, 3)
# 打印结果，如果属于red ,result中属于0 label;如果是blue,就是result=1
print( "result:  {}\n".format(results) )
print( "neighbours:  {}\n".format(neighbours) )
print( "distance:  {}\n".format(dist) )
plt.show()

输出结果：

1
2
3
4
5
result:  [[ 1.]]

neighbours:  [[ 1.  1.  0.]]

distance:  [[   18.   145.  1109.]]

图像:

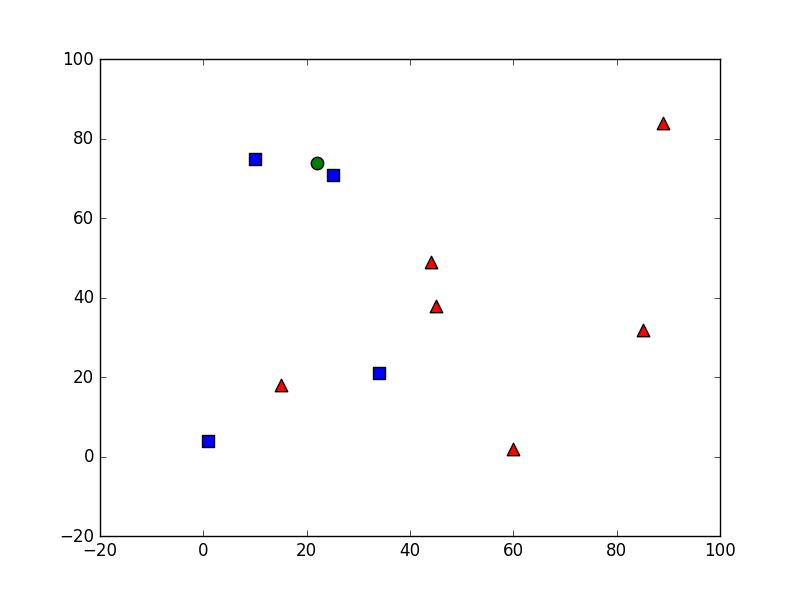
python_knn
从图像中可以看出，圆圈距离方块的距离较近，同时K=3，所以可以看到输出结果为label=1，也就是分到了blue方块类，所以result: [[ 1.]]，最近的三个元素分别为方块，方块，三角，所以neighbours: [[ 1. 1. 0.]]，三个元素到目标圆圈的距离为:distance: [[ 18. 145. 1109.]]

Donate comment here