LoG算子与DoG算子

LoG简介

图像中灰度变化较大的非连续像素可以看做是边缘，边缘是最为重要的图像特征之一，在目标检测、追踪、识别中都必不可少的使用到了边缘，人类视觉系统也对边缘信息非常敏感。
边缘检测的一般步骤如下：

滤波（去噪）
增强（一般是通过计算梯度幅值）
检测（在图像中有许多点的梯度幅值会比较大，而这些点并不都是边缘，所以应该用某种方法来确定边缘点，比如最简单的边缘检测判据：梯度幅值阈值）
定位（有些应用场合要求确定边缘位置，可以在子像素水平上来估计，指出边缘的位置和方向）

边缘检测方法比较常用的有基于各种算子的方法，有基于一阶导数的各种算子（Roberts、Sobel、Canny、Prewitt等），还有基于二阶导数的Laplacian算子（LoG）等。

LoG边缘检测算子是David Courtnay Marr和Ellen Hildreth（1980）共同提出的。因此，也称为边缘检测算法或Marr & Hildreth算子。该算法首先对图像做高斯滤波，然后再求其拉普拉斯（Laplacian）二阶导数。即图像与 Laplacian of the Gaussian function 进行滤波运算。最后，通过检测滤波结果的零交叉（Zero crossings）可以获得图像或物体的边缘。因而，也被业界简称为Laplacian-of-Gaussian (LoG)算子。

Marr和Hildreth证明了以下两个观点：

灰度变化与图像尺寸没有关系，因此检测需要不同尺度的算子
灰度的突然变化会在一阶导数中引起波峰和波谷，或者二阶导数中一起零交叉

其中一阶导数一般找梯度极值。二阶导数找过零点（需要忽略无意义的过零点（即均匀零区））。

LoG边缘检测算法步骤：

平滑：高斯滤波器
增强：Laplacian算子计算二阶导
检测：二阶导零交叉点并对应于一阶导数的较大峰值
定位：线性内插

根据卷积的求导法则，先卷积后求导和先求导后卷积是相等的，所以可以把第1、2步合并为一步，先对高斯滤波器做拉普拉斯变换，得到LoG算子，然后再用这个算子与图像做卷积。

探测器

灰度的突然变化会在一阶导数中引起波峰或者波谷，或者在二阶导数中等效的引起零交叉。

一阶微分探测器
从数学上讲，像素的灰度值变化速率，可以用一阶微分来检测，对于二维离散函数，其微分可以表示为： $\frac{\partial f(x,y)}{\partial x} = f(x+1,y) - f(x,y)\qquad$ $\frac{\partial f(x,y)}{\partial y} = f(x,y + 1) - f(x,y)\qquad$
二阶微分检测器
二阶微分同样可以如一阶微分一样，检测到函数的变化。二阶微分其实就是拉普拉斯算子，一般使用下面的方法表示：（两个方向）

$\nabla^{2}f = \frac{\partial^{2}f}{\partial{x^{2}}} + \frac{\partial^{2}f}{\partial{y^{2}}}$

为了适应图像处理，我们将拉普拉斯算子写成离散形式，其中

$\frac{\partial^{2}f}{\partial{x^{2}}} = f(x+1,y)+f(x-1,y)-2f(x,y)$ $\frac{\partial^{2}f}{\partial{y^{2}}} = f(x,y+1)+f(x,y-1)-2f(x,y)$

最终结果为:(两个方向作和)
\begin{equation}
\begin{aligned}
\frac{\partial^{2}f}{\partial{x^{2}}} + \frac{\partial^{2}f}{\partial{x^{2}}}&= f(x+1,y)+f(x-1,y)-2f(x,y) + f(x+1,y)+f(x-1,y)-2f(x,y)\&= f(x+1,y)+f(x-1,y) + f(x+1,y)+f(x-1,y) - 4f(x,y)
\nonumber
\end{aligned}
\end{equation}

所以拉普拉斯算子在图像处理中的模板为：

$\left[ \begin{matrix} 0 & 1 & 0 \\ 1 & -4 & 1 \\ 0 & 1 & 0 \end{matrix} \right]$

拉普拉斯算子对噪声和离散点极为敏感，所以在利用其进行边缘检测的时候，需要首先对图像进行平滑，除去噪声的影响。因为高斯运算和拉普拉斯运算可以叠加，我们可以将其的最终形式写为：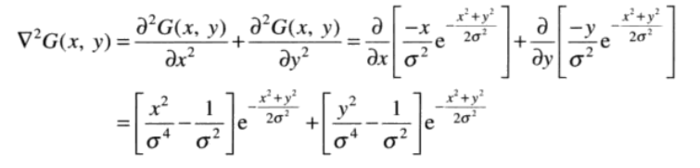
LoG公式推导
最终简化为: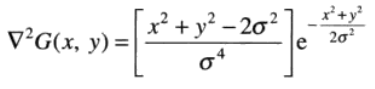

MatLab中的样子

laplace_gaussian_filter = fspecial('log',[40 40],4.5);
subplot(121)
surf(laplace_gaussian_filter);
subplot(122)
surf(-laplace_gaussian_filter);

LoG

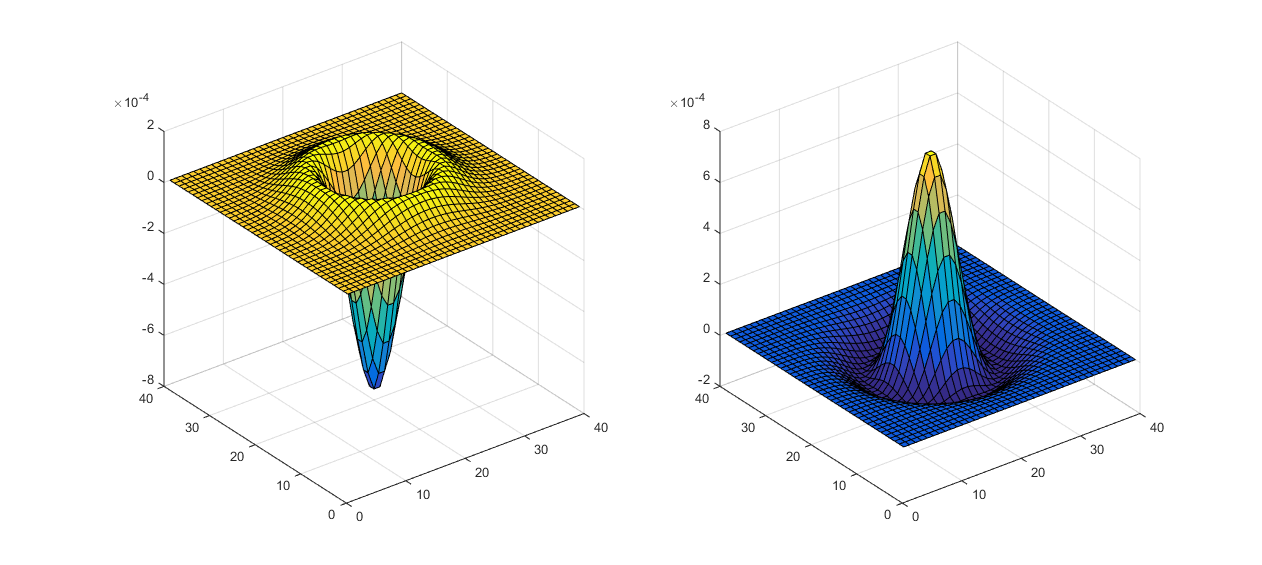
DoG简介

在计算机视觉中，高斯差（英语：Difference of Gaussians，简称“DOG”）是一种将一个原始灰度图像的模糊图像从另一幅灰度图像进行增强的算法，通过DOG以降低模糊图像的模糊度。这个模糊图像是通过将原始灰度图像经过带有不同标准差的高斯核进行卷积得到的。用高斯核进行高斯模糊只能压制高频信息。从一幅图像中减去另一幅可以保持在两幅图像中所保持的频带中含有的空间信息。这样的话，DOG就相当于一个能够去除除了那些在原始图像中被保留下来的频率之外的所有其他频率信息的带通滤波器。

DoG的数学含义

高斯函数的定义为：

$G_{\sigma_{1}}(x,y)=\frac{1}{\sqrt{2\pi\sigma^{2}_{1}}}\exp(-\frac{x^{2}+y^{2}}{2\sigma^{2}_{1}})$

我们知道，对于高斯金字塔的构建，就是对于不同尺度下的相同图片进行不同的 $\sigma$ 参数下的滤波操作，看下图中的左侧，就是对原图像进行了不同 $\sigma$ 高斯滤波的图像，对一副图像进行高斯滤波操作，在数学上就是高斯函数与原函数做卷积运算，从而得到高斯模糊图像，例如分别为$\sigma{1},\sigma{2}$ :

$g_{1}(x,y)=G_{\sigma_{1}}(x,y)*f(x,y)$ $g_{2}(x,y)=G_{\sigma_{2}}(x,y)*f(x,y)$

而右侧的DoG图像(高斯差分图像)就是左侧两个不同的高斯模糊图像做差得到的，高斯差分的数学表达：（上图中的两式相减）

$g_{1}(x,y)-g_{2}(x,y)=G_{\sigma_{1}}(x,y)*f(x,y)-G_{\sigma_{2}}(x,y)*f(x,y)=DoG*f(x,y)$

所以，上述公式可以将 $DoG$ 表示为：

$DoG = G_{\sigma_{1}}-G_{\sigma_{2}}=\frac{1}{\sqrt{2\pi}}(\frac{1}{\sigma_{1}}e^{-\frac{(x^{2}+y^{2})}{2\sigma^{2}_{1}}}-\frac{1}{\sigma_{2}}e^{-\frac{(x^{2}+y^{2})}{2\sigma^{2}_{2}}})$

这样，右侧就得到了高斯差分（DoG）图像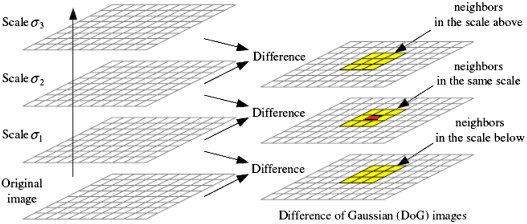
DoG

得到DoG图像后，再在DoG图像上检测特征，提取特征，这样做的好处就是，既能降低计算成本，又能不损失特征，不同的高斯平滑后得到的DoG图像都是明显的特征点。

DoG的应用

作为一个增强算法，DOG可以被用来增加边缘和其他细节的可见性，大部分的边缘锐化算子使用增强高频信号的方法，但是因为随机噪声也是高频信号，很多锐化算子也增强了噪声。DOG算法去除的高频信号中通常包含了随机噪声，所以这种方法是最适合处理那些有高频噪声的图像。这个算法的一个主要缺点就是在调整图像对比度的过程中信息量会减少。

当它被用于图像增强时，DOG算法中两个高斯核的半径之比通常为4:1或5:1。当设为1.6时，即为高斯拉普拉斯算子的近似。高斯拉普拉斯算子在多尺度多分辨率像片。用于近似高斯拉普拉斯算子两个高斯核的确切大小决定了两个高斯模糊后的影像间的尺度。

DOG也被用于尺度不变特征变换中的斑点检测。事实上，DOG算法作为两个多元正态分布的差通常总额为零，把它和一个恒定信号进行卷积没有意义。当K约等于1.6时它很好的近似了高斯拉普拉斯变换，当K约等于5时又很好的近似了视网膜上神经节细胞的视野。它可以很好的作为一个实时斑点检测算子和尺度选择算子应用于递归程序。

在DOG算法中，它被认为是在模拟视网膜上的神经从影像中提取信息从而提供给大脑。