SIFT尺度不变特征变换

发表于 | 分类于

通过上一篇文章，我们了解到了一些角点探测器，如 Harris Corner Detection 等。它们是旋转不变的，这意味着，即使图像旋转了，我们也可以找到相同的角点。这是显而易见的，因为角落在旋转的图像中也是角点。但是缩放呢？如果图像缩放，角点可能不是角点。例如，请查看下面的简单图片。放大同一个窗口时，小窗口内的小图像中的一个角点变成平坦的。所以Harris Corner的角点不是尺度不变的。

sift_scale_invariant

因此，2004年，不列颠哥伦比亚大学的D.Lowe在他的论文中提出了一种新的算法 - 尺度不变特征变换（SIFT），该算法从尺度不变关键点获取独特的图像特征，提取关键点并计算其描述符。

SIFT算法主要涉及四个步骤。我们将逐一分析他们。

Scale-space Extrema Detection 尺度空间极值检测

从上图中可以看出，我们不能使用相同的窗口来检测不同尺度下图片上的关键点。上图中，用来检测小图像中的角点还能使用，但是如何检测大尺度图片下的角点，我们就需要更大的窗口函数，因此，我们需要尺度空间滤波。其中，Laplacian of Gaussian（LoG） 就是为具有不同 $\sigma$ 值的图像而创建的。LoG 作为一个斑点探测器（a blob detector），可以检测由于 $\sigma$ 变化而产生的各种尺寸的斑点。简而言之，$\sigma$ 的作用就是一个缩放参数。也就是说当 $\sigma$ 较小的时候，表示高斯核拥有较小的高斯核，适合探测较小尺寸图片上的角点；当 $\sigma$ 较大的时候，表示该高斯核适合探测较大图片尺寸上的角点。

因此，我们探测一个图片的角点就需要三个参数 $(x,y,\sigma)$ 这意味着在 $\sigma$ 尺度下 $(x,y)$ 是候选关键点。

但是LoG算法的算法开销略大，所以SIFT选用了Difference of Gaussians （DoG——高斯差分）。DoG图像的获得是由两个不同高斯模糊的图像（——例如一个为 $\sigma$, 另一个为 $k\sigma$，也就是不同尺寸的同一张图像）作差差而得到的，这个DoG图像叫做：高斯差分图像。这个过程在高斯金字塔下完成：

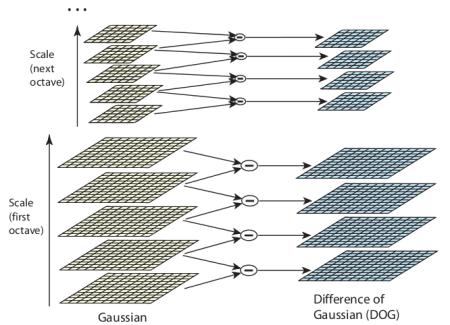
sift_dog

从上图可以看出，左侧是不同尺度，不同分辨率的原图像构成的图像金字塔，（一般把原图像放大一倍作为第一组，然后每一组中又有多个图像构成的层，同一组中的不同层的区别是高斯模糊的程度，然后组跟组之间的关系为：第二组中的第一层的图像是选取的第一组中的倒数第三层图像，依次类推；同时第二组跟第一组比图像大小上依次尺度降低为上一层的二分之一，长宽各变为原来的一半）。

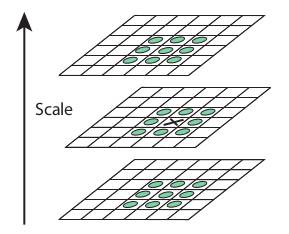
一旦找到这个DoG图像，就会在尺度和空间中搜索该DoG图像的局部极值。（具体的实现过程下面会介绍）从下面图像中可以看到，对于DoG图像，对于某个像素处，我们要判断它是否是我们要找的局部极值点。方式是提取图中的 × 点处周围的26个点（它所在的DoG图中的周围8个点，它上下两层相邻的各9个点），进行比较，如果是极值（局部极值），就当做一个候选点（潜在关键点）。

sift_local_extrema

所以整个流程如下图：

Keypoint Localization 关键点定位

候选点（潜在关键点）被找到后，需要确定更高精度的极值的。文章中使用了尺度空间的Taylor展开来获取这个更加准确的极值，如果这个极值的大小小于给定的阈值（Paper中的阈值为：0.03），这个极值就会被拒绝，也就是说候选点被舍弃。这个阈值在OpenCV中被称作 contractThreshold。

DoG 对图像的边缘也有很高的响应，所以也要想办法把图像边缘过滤掉，为此，论文中使用了类似于Harris角点探测的概念——使用2x2的Hessian矩阵（H）来计算曲率，我们从Harris角点探测的文章中了解到，一个特征值比另一个特征值大很多的时候，这时表示的是边缘，回顾如下图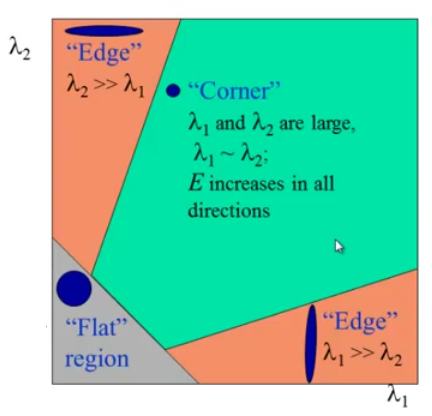：harris_region 这里文中也使用了简单的探测函数。

这样以后，消除了一部分候选点和边缘，剩下的是原图中的强兴趣点（原文叫做 strong interest point，这。。怎么翻译？）。

Orientation Assignment （梯度）方向赋值

现在为每个关键点赋值一个方向，以实现图像的旋转不变性，在当前尺度下确定一个关键点的邻域，并在该区域计算梯度方向。具体方法为：创建一个具有36个方向的方向直方图，每个方向相隔10度，这样36个方向可以覆盖360度。如下图中的右图。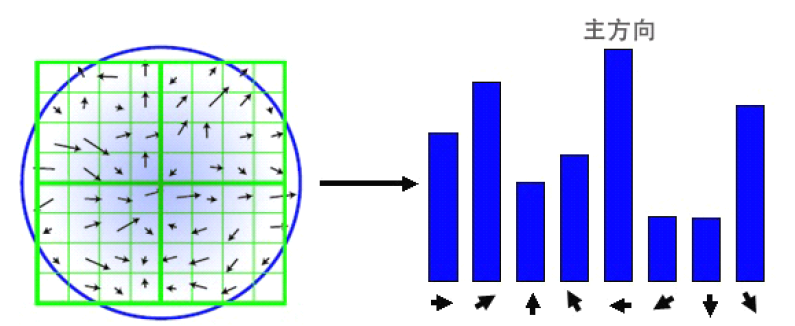
orientation
图中左侧是关键点圆形邻域内的所有分割，这些区域都有自己的方向梯度，然后将每个区域的方向梯度在相同方向加和，分列在直方图的各个方向上，纵轴就是该点各方向梯度和的值。最高的那个就是该关键点的主梯度方向。当然有可能一个点处有多个方向梯度，就是该点向多个方向的灰度梯度都比较大，体现在直方图中就是会有多个方向的值都很高，所以一个点有主梯度方向，也可以有辅梯度方向。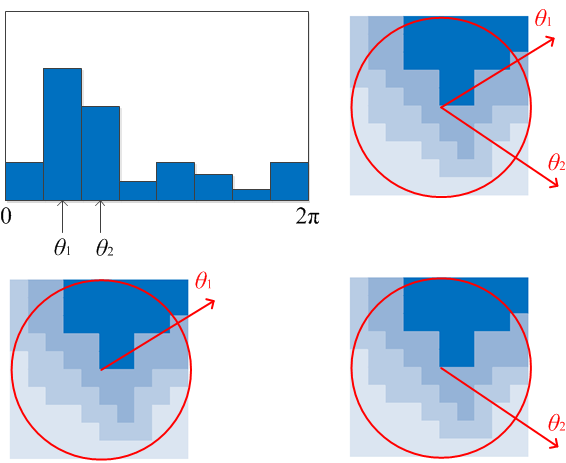
Orientation_second.jpg

Keypoint Descriptor 关键点描述符

找到了关键点的梯度方向，下一步就是要描述这些关键点了，与求该点主方向不同的是，如下图中的左侧，关键点划分成16x16的区域，它被划分为16个4x4的子块。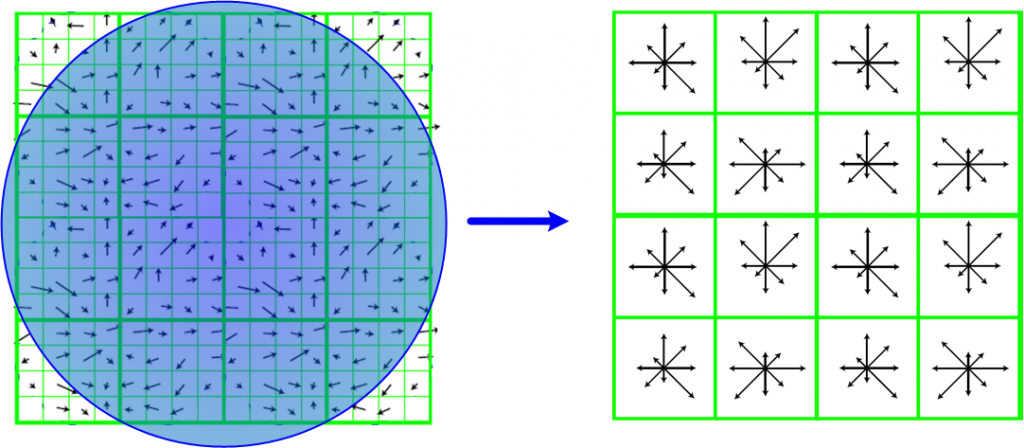
keypoint
下一步工作就是，针对每一个4x4的子块，创建一个具有8个方向（每隔45°一个方向）的直方图，即这个区域的8个方向的梯度强度。这样16个子块就会有 8x16=128 个梯度强度信息数据，这也就是SIFT的128维特征矢量。
除此之外，还采取了几项措施来实现对光照变化，旋转等的鲁棒性。

Keypoint Matching 关键点匹配

两幅图像之间的关键点的匹配工作是通过判断他们的最近邻域来实现的。但在某些情况下，第二最近邻域可能比最近邻域匹配的更好。（这个地方该怎么翻译？总感觉不对 Keypoints between two images are matched by identifying their nearest neighbours. But in some cases, the second closest-match may be very near to the first.）这可能是由于噪音或其他原因产生的。在这种情况下，需要计算最近距离与第二近距离的比值，如果这个比值大于0.8，则这个第二最近距离就被舍弃。
这个理解如下：
pointmatch
计算量上，如果我们有10个待匹配点，那么计算量就是$10^{2}$;

使用

SIFT被申请了专利，所以原文中的算法放在了the opencv contrib repo。

1
2
3
4
5
6
7
8
import numpy as np
import cv2 as cv
img = cv.imread('home.jpg')
gray= cv.cvtColor(img,cv.COLOR_BGR2GRAY)
sift = cv.xfeatures2d.SIFT_create()
kp = sift.detect(gray,None)
img=cv.drawKeypoints(gray,kp,img)
cv.imwrite('sift_keypoints.jpg',img)

sift.detect()函数用来在图像中查找关键点，OpenCV还提供cv.drawKeyPoints()函数，用于在关键点位置上绘制小圆圈。

1
2
img=cv.drawKeypoints(gray,kp,img,flags=cv.DRAW_MATCHES_FLAGS_DRAW_RICH_KEYPOINTS)
cv.imwrite('sift_keypoints.jpg',img)

图例：
sift_keypoints
计算特征描述符，OpenCV提供了两种方法：

  1. 既然你已经找到了关键点，你可以调用sift.compute()来计算我们找到的关键点的描述符。例如：kp,des = sift.compute(gray,kp)
  2. 如果还没有找到关键点，可以使用如下方法将寻找关键点和计算描述符合并为一步：sift.detectAndCompute()

在OpenCV中:

1
2
sift = cv.xfeatures2d.SIFT_create()
kp, des = sift.detectAndCompute(gray,None)

这里kp是一个关键点列表，des是一个形为$Number_of_Keypoints×128$的numpy数组。

至此我们获得了关键点，描述符等等，SIFT的基本概念也了解了。如何匹配不同图像中的关键点呢？后续文章中将会学习。

其他知识储备

角点

尺度规范化的LoG算子

Lowe使用DoG图像

高斯差分图像

拟合三维二次函数

图像灰度

归一化处理

非线性光照

相机饱和度

coding+pooling线路

BOW（Bag of Word），VLAD，SCP以及我们使用的LLC（Locality-constrained Linear Coding）

sparse

匹配与选取

RANSAC

相似分计算

SURF、Color-SIFT、Affine-SIFT、Dense-SIFT、PCA-SIFT、Kaze

Donate comment here