上一篇文章介绍了什么是特征,本篇介绍一下如何提取特征(角点特征)
特征点检测广泛应用到目标匹配、目标跟踪、三维重建等应用中,在进行目标建模时会对图像进行目标特征的提取,常用的有颜色、角点、特征点、轮廓、纹理等特征。
上一篇文章当中,我们学习到了对于一个图像,图像的角落是比较适合作为特征的区域,是各个方向上强度变化较大的区域。早在一九八八年(1988年老子还特么没出生呢!人家就开始研究这些东西了。。。这个领域到底跟美国有多大差距啊!!),Chris Harris&Mike Stephens早期在其论文《A Combined Corner and Edge Detector》中就尝试去发现了这些角落,并把它称为Harris Corner Detector。Harris角点检测是通过数学计算在图像上发现角点特征的一种算法,而且其具有旋转不变性的特质。它的原理就是找到滑动窗口内的点,然后这个点向各个方向上的灰度差最明显的地方(实际就是一阶导数最大的地方)。OpenCV中的Shi-Tomasi角点检测就是基于Harris角点检测改进算法。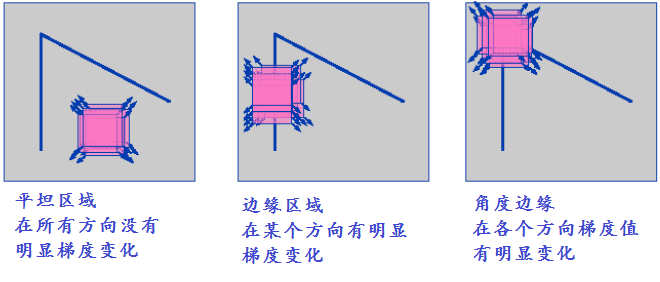
他把这个简单的想法变成了一种数学形式。这个表达式如下:
其中 $W(x, y)$ 表示移动窗口,$I(x, y)$ 表示像素灰度值强度,范围为 0~255。根据泰勒级数
计算一阶到N阶的偏导数,最终得到一个Harris矩阵公式:
Window function是给对应的 $x,y$ 像素加权的矩形窗口或高斯窗口。对于角点检测,我们必须使得$E(u,v)$取得最大值。这样就意味着,对于上面的公式,我们必须使得等号后的第二项最大化(中括号内的项),运用泰勒展开式并使用一些数学过程,我们能够最终得到下列方程:
同时:
这里$I{x}$ 和 $I{y}$ 是图像在 $x$ 和 $y$ 方向上的导数,(能够简单的通过cv.Sobel()方法得到)。
然后是主要部分,这帮人又创建了一个得分数,它将决定一个窗口是否可以包含角点。
and
- $det(M) = \lambda{1}\lambda{2}$ (是行列式)
- $trace(M) = \lambda{1} + \lambda{2}$ (是矩阵的迹)
- $\lambda{1}$ and $\lambda{2}$ (是M的特征值)
通过上面的公式可以确定的是特征值决定了我们找到的这个区域中是包含的角点,边缘,还是平面。
- 当 $|R|$ 是比较小的值的时候,也就是 $\lambda{1}$ and $\lambda{2}$ 很小,则表示这个区域是平坦的。
- 当 $R < 0$ 时,只有当 $\lambda{1} >> \lambda{2}$ 或者 $\lambda{2} >> \lambda{1}$ 时才会发生,此时表示这块区域是边缘。
- 当 $R$ 是非常大的值的时候,只有当 $\lambda{2}, \lambda{2}$ 都比较大而且 $\lambda{1}\sim\lambda{2}$ 的时候这个区域表示角点。
上面的表述可以用一张图片来表示
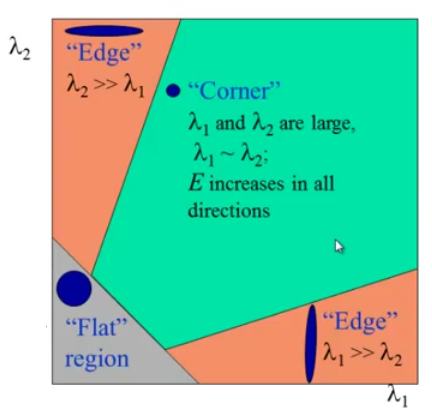
上图中的横向和纵向分别可以看作是$\lambda{1}$ 和 $\lambda{2}$ 的坐标,不要把当作是个正方形。
哈里斯角点(角落)检测的结果是一个具有得分数的灰度图像。合适的阈值会帮助我们找到图像中的角点。我们将会以一个简单的例子说明。
Harris Corner Detector 在 OpenCV 中的应用
OpenCV中有cv.cornerHarris(),它的参数分别是:
- img - Input image, 应该是32位的灰度图.
- blockSize - 考虑角点检测的邻域的大小.
- ksize - 使用Sobel导数的光圈参数
- k - 方程中Harris detector的自由参数.
example:
1 | import numpy as np |
结果如下:

Corner with SubPixel Accuracy (具有子像素准确度的角点)
有时候,你可能需要以最高的精度找到角点,OpenCV提供了可以进一步细化像素检测角点的函数cv.cornerSubPix(),首先还是要先找到 Harris Corner 然后通过这些角点的质心来优化它们,下图中,Harris Corner是红色像素,精确角点为绿色像素。我们指定迭代次数或达到一定的准确度后停止,(二者以先发生者为准)。我们还需要定义要搜索拐角的邻域的大小。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22import numpy as np
import cv2 as cv
filename = 'chessboard2.jpg'
img = cv.imread(filename)
gray = cv.cvtColor(img,cv.COLOR_BGR2GRAY)
# find Harris corners
gray = np.float32(gray)
dst = cv.cornerHarris(gray,2,3,0.04)
dst = cv.dilate(dst,None)
ret, dst = cv.threshold(dst,0.01*dst.max(),255,0)
dst = np.uint8(dst)
# find centroids
ret, labels, stats, centroids = cv.connectedComponentsWithStats(dst)
# define the criteria to stop and refine the corners
criteria = (cv.TERM_CRITERIA_EPS + cv.TERM_CRITERIA_MAX_ITER, 100, 0.001)
corners = cv.cornerSubPix(gray,np.float32(centroids),(5,5),(-1,-1),criteria)
# Now draw them
res = np.hstack((centroids,corners))
res = np.int0(res)
img[res[:,1],res[:,0]]=[0,0,255]
img[res[:,3],res[:,2]] = [0,255,0]
cv.imwrite('subpixel5.png',img)
结果如下: (一些关键点可能需要放大来看)
![]()
至此Harris Corner Detection就介绍完了。
总结
Harris角点检测是特征点检测的基础,提出了应用邻近像素点灰度差值概念,从而进行判断是否为角点、边缘、平滑区域。Harris角点检测原理是利用移动的窗口在图像中计算灰度变化值,其中关键流程包括转化为灰度图像、计算差分图像、高斯平滑、计算局部极值、确认角点。在特征点检测中经常提出尺度不变、旋转不变、抗噪声影响等,这些是判断特征点是否稳定的指标。
总的来说通过看公式
第一项是窗口函数,第二项是灰度梯度,也就是灰度变化的导数,$x$,$y$ 决定了各个方向,而后窗口函数是矩形窗口函数,或者高斯窗口函数。这是因为:矩形窗口函数可以过滤掉图像边缘,因为边缘出去在边缘方向的梯度是很小的,其他方向梯度也很大;高斯窗口函数可以过滤掉凸点或者一些孤立点,因为凸点和孤立点的各个方向的梯度也很大。
这两个结合使用就可以选出角点(图像上拐角的地方)。
问题与后续发展
- 后续又出现了Harris Corner的改进版:Shi-Tomasi Corner Detection
- Harris Corner是旋转不变的,但是不是尺度不变的,因为探测窗口的大小不变的情况下,放大图像后,原来的角点有可能变成平滑的,如下图:
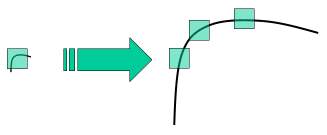
- 为了找到旋转,尺度都不变的探测器,由此诞生了SIFT。

